|
For the second approach, the evolution of a model without directly using random constants, the set of fitness cases and the function set were as in
section 3.1.1, and T = {a}. The parameters used per run are shown in the second column of
Table 4. In this experiment of 100 identical runs, the best solution was found in generation 1210 of run 63:
|
01234567890120123456789012012345678901201234567890120123456789012 |
|
|
+EL-*/aaaaaaa~a+E/Laaaaaaa+C+C+Eaaaaaaa*C~+aSaaaaaaa~a-L~+aaaaaaa |
(3.5) |
It has a fitness of 1982.488 and an R-square of 0.99996922 evaluated over the set of 20 fitness cases and an R-square of 0.9999460 evaluated against the same test set of
section 3.1.1, and thus is better than the model
3.4 evolved with the facility for creation of random constants. This model is also an almost perfect match for the
target function. Its expression is shown in
Figure 16.
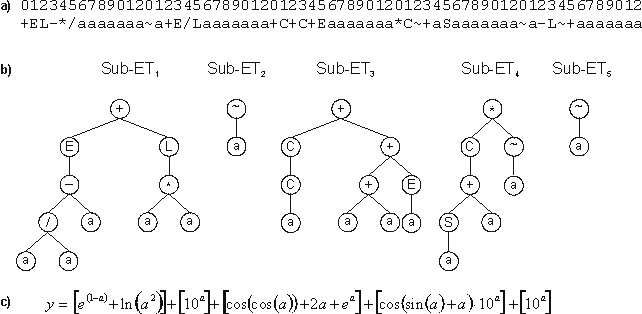
Figure 16. Model evolved by GEP without explicitly using random constants.
a) The model in Karva notation. b) The sub-ETs codified by each gene.
c) The corresponding mathematical expression after linking with addition (the contribution of each sub-ET is shown in square brackets).
Once again, the plots of the target
function and the model 3.5 evolved by GEP are compared in
Figure 17.
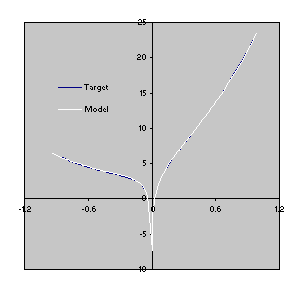
Figure 17. Comparison of the target function with the model
3.5 evolved by GEP without explicitly using random constants
(Figure 16). The R-square was evaluated over the test set of 100 random points and is equal to 0.9999460.
It is instructive to compare the results obtained in both approaches. Not only the model
3.5 evolved without random constants was better than the model
3.4 evolved with random constants, but also the average best-of-run fitness was superior in the second approach: 1934.619 compared to 1850.476 (see
Table 4). Thus, in real-world applications where complex realities are modeled, of which it is impossible to infer neither the type nor the range of the numerical constants, and where most of the times we are unable to guess the exact function set, it is more appropriate to let the system model the reality on its own without explicitly using random constants. Perhaps the models would be unconventional comparatively to human-created ones, but they allow, nonetheless, the extraction of knowledge because the programs evolved by GEP are simple and accessible. It is worth noticing that some learning algorithms like neural networks do not allow knowledge extraction from their models whereas others produce so complicated models that their analysis is considerably limited.
|

