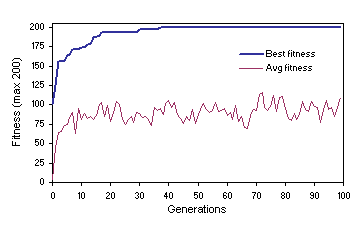
Figure 2. Evolutionary dynamics characteristic of non-homogenizing systems. In this case, the population evolved under a mutation rate of 0.05. Note the oscillatory pattern on average fitness and the wide gap between best and average fitness.


On the other hand, populations undergoing recombination alone have homogenizing dynamics [5]. In these populations, the gap between average and best fitness is considerably smaller and, with time, tends to disappear completely. Obviously, when this happens all the individuals in the population have the same genetic makeup and populations become stagnant and incapable of adaptation. Also important is the fact that the plot for average fitness does not show such dramatic oscillations as observed in populations with non-homogenizing dynamics. Note also that, in these systems, populations evolve very inefficiently (see Table 1).

The evolutionary dynamics presented in Figure 3 was obtained for populations subjected to three different kinds of recombination simultaneously (Table 1, column 5). Notwithstanding, these populations exhibit the same homogenizing effect described for populations undergoing only one type of recombination at a time. This further reinforces the hypothesis that recombination is conservative and, therefore, plays a major role at maintaining the status quo [5]. Note that, in this particular case, by generation 54 the plot for average fitness meets the plot for best fitness and all individuals become genetically identical. This might be seen as a good thing especially if all the individuals would have become equal and perfect. Recall, however, that in complex real-world problems, as in nature, perfection is always a step further ahead. The disadvantages of such an evolutionary strategy, however, become evident when average fitness reaches best fitness before a perfect or good solution is found. Figure 4 shows such a case where the population stabilized on a mediocre solution. In this case, after generation 86 adaptation becomes impossible because all individuals share the same genetic makeup. Indeed, the small success rates typical of populations undergoing recombination alone (see Table 1, for instance) indicate that, most of the times, homogenizing populations converge before finding a good solution because they became irrevocably stuck in some local point, not necessarily optimal.

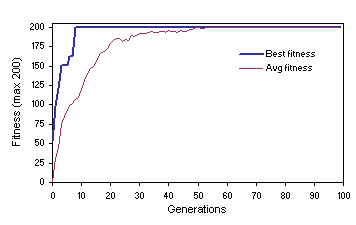
Figure 3. Evolutionary dynamics characteristic of homogenizing populations undergoing recombination. The rates of the three recombination operators used (two-point, one-point and gene recombination) were identical and equal to 0.8. Note the absence of dramatic oscillations on average fitness and that average fitness increases consistently until the complete loss of genetic diversity.


It is worth noticing that in the experiments summarized in Table 1, totally random initial populations were used and, therefore, the number of viable individuals in those initial populations was not controlled. In the next section it is shown how the number of viable individuals in initial populations can be rigorously controlled in order to analyze the founder effect in artificial evolutionary systems.

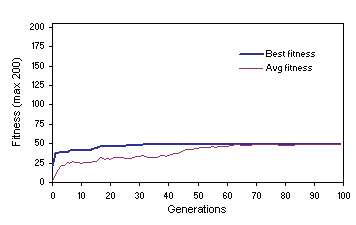
Figure 4. Convergence on a mediocre solution in homogenizing populations undergoing recombination alone. The parameters are exactly the same as in Figure 3.