where n consists of the nonnegative integers. This sequence was chosen for three reasons. First, it can be exactly solved by the algorithm and therefore provide an accurate measure of performance in terms of success rate. Second, it requires relatively small populations and relatively short evolutionary times, making the task feasible. And third, it provides sufficient resolution to allow the comparison of dissimilarly performing operators such as mutation and recombination.

In all the experiments, the first 10 positive integers n and their corresponding term were used as fitness cases; the fitness function was based on the relative error with a selection range of 20% and maximum precision (0% error), giving maximum fitness f_max = 200 [4]; the selection was made by roulette-wheel sampling coupled with simple elitism; population sizes P of 50 individuals and evolutionary times G = 100 generations were used; the success rate of each experiment was evaluated over 100 independent runs; F = {+, -, *, /} and the terminal set T consisted only of the independent variable which was represented by a, giving T = {a}; and six-genic chromosomes of length 78 (head length h = 6) linked by addition were used.

In gene expression programming mutation is by far the single most important genetic operator and populations undergoing mutation display non-homogenizing dynamics [5], i.e., the best fitness is always considerably above average fitness and average fitness displays a pronounced oscillatory pattern. Furthermore, mutation is the only operator capable of reaching the performance peak and, for each experiment, this peak can be found. Figure 1 shows the performance peak for populations evolving using the parameters given above. In this case, maximum performance is reached around a mutation rate p_m = 0.05. Therefore, this value will be used to study the importance of the initial diversity in non-homogenizing populations.

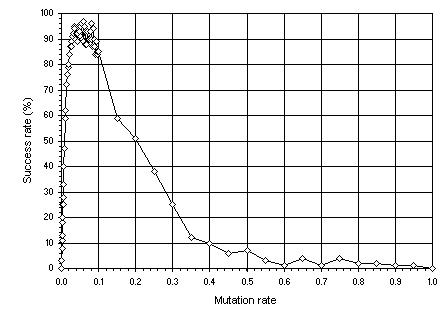
Figure 1. Determining the performance summit using mutation alone.


As for recombination, this operator is the less powerful of all GEP operators and populations undergoing recombination alone display homogenizing dynamics [5], i.e., with time, the best fitness becomes equal to average fitness and populations lose all genetic diversity. Furthermore, it has been shown that the three kinds of GEP recombination (two-point, one-point and gene recombination) perform better at maximum rates of 1.0, being two-point recombination the most powerful of the three recombinational operators and gene recombination the less powerful [5]. However, for the particular settings used in this analysis, when used separately, the three kinds of recombination perform so poorly that the three recombinational operators were combined together so that the performance of the algorithm increased a little (Table 1, column 5). As shown in the fifth column of Table 1, in this experiment, the recombination rates of the three recombinational operators are identical and equal to 0.8. Note that the success rate increases slightly comparatively to the individual performances obtained for the recombination operators working separately. So, the dependence of success rate on the number of actual founders in populations undergoing recombination will be analyzed using the general settings shown in the fifth column of Table 1. As will next be shown, the kind of evolutionary dynamics exhibited by these populations is, nonetheless, of the same kind as the homogenizing dynamics characteristic of populations undergoing only one type of recombination at a time.


Table 1
Success rates and parameters for a non-homogenizing system undergoing mutation (Mut) and homogenizing systems undergoing two-point recombination (Rec2P), one-point recombination (Rec1P), gene recombination (RecG), and three different kinds of recombination (RecMix).