The question of the initial diversity is one of interest in artificial evolutionary systems as a considerable amount of computational resources could go into guaranteeing the adequate initial diversity for populations to evolve efficiently. Here, two different systems will be compared: one that relies on mutation and has a non-homogenizing evolutionary dynamics and another that relies exclusively on crossover and, therefore, has a homogenizing dynamics.
For this analysis, a smaller, totally random “initial” population (founder population) composed of a certain number of viable individuals is created. That is, the run only starts when all the members of the founder population are viable, that is, have positive fitness. These founder individuals are afterwards selected and reproduced, leaving as many descendants as the actual population size
P.
As shown in Figure 5, for non-homogenizing populations there is no correlation between success rate and the initial diversity. Indeed, due to the constant introduction of genetic modification in the population, in non-homogenizing populations, after a certain time, the founder effect is completely erased and populations evolve, as usual, efficiently.
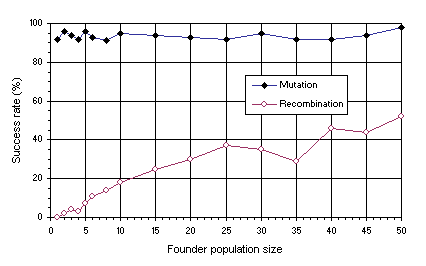
Figure 5. Dependence of success rate on the size of the founder population in non-homogenizing populations undergoing mutation alone (mutation rate equal to 0.05) and homogenizing populations undergoing recombination alone (two-point, one-point and gene recombination rates all equal to 0.8).
However, a very different situation happens in populations where crossover is the only source of genetic diversity and the evolutionary dynamics are homogenizing in effect. In these cases, there is a strong correlation between success rate and initial diversity. Note that populations evolve poorly under recombination, being practically incapable of adaptation in the cases where only 2-5 founder individuals are used (obviously, for cases with only one founder, homogenizing populations are altogether incapable of adaptation). It is worth emphasizing that, in these systems, even when the size of the founder population is equal to
P, the success rate is significantly smaller than in populations undergoing mutation, with only one viable individual in the founder population.
Also worth considering is that the computational resources required to guarantee the creation of large founder populations are very expensive. Thus, systems such as GEP capable of evolving efficiently with minimal initial diversity are most advantageous. Furthermore, for some complex problems like, for instance, the discovery of cellular automata rules for the density-classification task
[4], it is very difficult to generate randomly a viable individual, even a mediocre one, to start the run. In those cases, systems like GEP can use this individual as founder and continue from there, whereas systems relying on recombination alone will be stuck for a long time before they gather momentum. In GEP, due to the varied set of genetic operators available such as the high-performing point mutation and transposition, there is no need for large founder populations because as long as one viable individual is randomly generated in the initial population the evolutionary process can get started.
|
