In block stacking, the goal is to find a plan that takes any initial configuration of blocks randomly distributed between the stack and the table and places them in the stack in the correct order. In this case, the blocks are the letters of the word “universal”. (Although the word universal was used as illustration, in this version the blocks being stacked may have identical labels like, for instance, in the word “individual”.)

The functions and terminals used for this problem consisted of a set of actions and sensors, being F = {C, R, N, A} (move to stack, remove from stack, not, and do until true, respectively), where the first three take one argument and “A” takes two arguments. In this version, the “A” loops are processed at the beginning and are solved in a particular order (from bottom to top and from left to right). The action argument is executed at least once despite the state of the predicate argument and each loop is executed only once, timing out after 20 iterations. The set of terminals consisted of three sensors {u, t, p} (current stack, top correct block, and next needed block, respectively). In this version, “t” refers only to the block on the top of the stack and whether it is correct or not; if the stack is empty or has some blocks, all of them correctly stacked, the sensor returns True, otherwise it returns False; and “p” refers obviously to the next needed block immediately after “t”.

A multigenic system composed of three genes of length 9 was used in this problem. The linking of the sub-ETs consisted of the sequential execution of each sub-ET or sub-plan. For instance, if the first sub-ET empties all the stacks, the next sub-ET may proceed to fill them, and so on. The fitness was determined against 10 fitness cases (initial configurations of blocks). For each generation, an empty stack plus nine initial configurations with one to nine letters in the stack were randomly generated. The empty stack was used to prevent the untimely termination of runs, as a fitness point was attributed to each empty stack (see below). However, GEP is capable of efficiently solving this problem using 10 random initial configurations (results not shown).

The fitness function was as follows: for each empty stack one fitness point was attributed; for each partially and correctly packed stack (i.e., with 1 to 8 letters in the case of the word “universal”) two fitness points were attributed; and for each completely and correctly stacked word 3 fitness points were attributed. Thus, the maximum fitness was 30. The idea was to make the population of programs hierarchically evolve solutions toward a perfect plan. And, in fact, usually the first useful plan discovered empties all the stacks, then some programs learn how to partially fill those empty stacks, and finally a perfect plan is discovered that fills the stacks completely and correctly (see Figure 13).

Figure 13 shows the progression of average fitness of the population and the fitness of the best individual for run 2 of the experiment summarized in Table 2, column 4. In this run, a perfect plan was found in generation 50:

012345678012345678012345678
ARCuptppuApNCptuutNtpRppptp

Note that the first sub-plan removes all the blocks and stacks a correct letter; the second sub-plan correctly stacks all the remaining letters; and the last sub-plan does nothing. It should be emphasized that the plans with maximum fitness evolved are in fact perfect, universal plans: each generation they are tested against nine randomly generated initial configurations, more than sufficient to allow the algorithm to generalize the problem (as shown in Figure 13, once reached, the maximum fitness is maintained). Indeed, with the fitness function and the kind of fitness cases used, all plans with maximum fitness are universal plans.

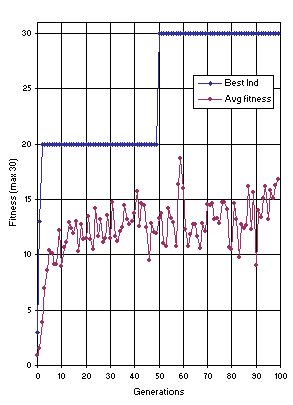
Figure 13. Progression of average fitness of the population and the fitness of the best individual for run 2 of the experiment summarized in Table 2, column 4 (block stacking).

As shown in the fourth column of Table 2, the probability of success for this problem is very high (0.70) despite using nine (out of 10) random initial configurations. It is worth noting that GP uses 167 fitness cases, cleverly constructed to cover the various classes of possible initial configurations [9]. Indeed, in real-life applications it is not always possible to predict the kind of cases that would make the system discover a solution. So, algorithms capable of generalizing well in face of random fitness cases are more advantageous.