For the TSP with 19 cities there are 19! = 1.21645X10¹⁷ combinations to search. If the starting point is fixed (and consequently the ending point), the number of possible combinations is halved to 6.0823X10¹⁶. Furthermore, choosing a configuration where all the cities lie in a rectangle so that the shortest tour is 20, allows the rigorous evaluation of the performance of the algorithm in terms of success rate.

Obviously, the tour length cannot be used directly as a measure of fitness as the shorter the tour the fitter the individual. Thus, each generation, the fitness f_i of an individual program i in generation g is evaluated by the formula:

where t_i is the length of the tour encoded in i, and T_g is the length of the largest tour encoded in the chromosomes of the current population. This way, the fitness of the worst individual of the population is always 1. As usual in GEP, individuals are selected according to fitness by roulette-wheel selection and each generation the best individual is cloned unchanged into the next generation (simple elitism). The parameters used per run are summarized in the first column of Table 1.

Table 1
Parameters for the traveling salesperson problem with 19 cities (TSP) and for the task assignment problem (TAP).

The results obtained by GEP are astounding if we compare them with the performance of GAs to solve the 19-cities tour TSP. As a comparison, Haupt and Haupt (1998) could not solve this problem using population sizes of 800 for 200 generations. As shown in Figure 1 and in the first column of Table 1, GEP not only is capable of solving this problem using populations of only 100 individuals and for the same 200 generations, but also is capable of finding the shortest route in practically all runs (in 96% of the runs, in fact).

It is worth emphasizing that only inversion was used to create genetic variation. And, indeed, the presence of other genetic operators, namely gene deletion/insertion and restricted permutation, decreases slightly the success rate and therefore were not used. It seems that these operators are unnecessary for finer adjustments whenever inversion is doing the search.

Figure 4 shows the progression of average and best tour for a successful run of the experiment summarized in the first column of Table 1. Note that the evolutionary dynamics for combinatorial problems is similar to the dynamics characteristic of GAs (see, e.g., Goldberg 1989). In these dynamics the plot for average fitness closely accompanies the plot for best fitness and the oscillatory pattern on average fitness is less pronounced than in GEP dynamics (Ferreira 2002). The dynamics obtained here support the idea that simple replicator systems are fundamentally different from genotype/phenotype systems where a complex expression already exists. Indeed, an extremely simple expression takes place to express fully the chromosomes used to solve the TSP: in fact, the chromosome itself is the phenotype or the solution.

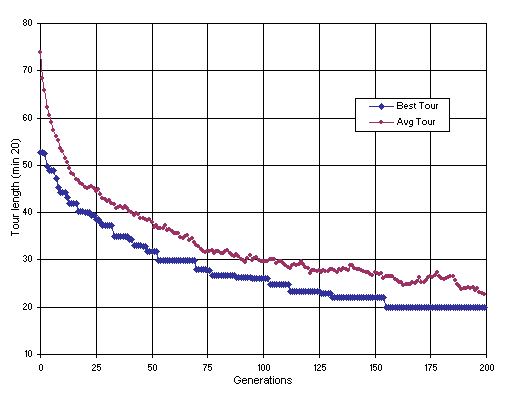
Figure 4. Progression of average tour of the population and the best tour for a successful run of the experiment summarized in the first column of Table 1 (TSP with 19 cities).