Combinatorial-specific Operators: Performance and Mechanisms

  GEP Book

  Home
  News
  Author
  Q&A
  Tutorials
  Downloads
  GEP Biblio
  Contacts

  Visit Gepsoft

C. FERREIRA

In J. M. Santos and A. Zapico, eds., Proceedings of the Argentine Symposium on Artificial Intelligence, pages 160-174, Santa Fe, Argentina, 2002.

Combinatorial Optimization by Gene Expression Programming: Inversion Revisited

Combinatorial problems can not be solved using the genetic operators of mutation and recombination of the basic gene expression algorithm as these operators would generate useless individuals containing MGFs with repeated elements on the one hand, and missing certain elements on the other. Indeed, in combinatorial problems, the elements of a multigene family must all be present and cannot be represented more than once. Therefore, special search operators must be created so that genetic variation could be introduced without creating invalid structures.

In this section, five genetic operators are described: inversion, gene and sequence deletion/insertion, and restricted and generalized permutation. These combinatorial-specific operators allow the introduction of genetic variation without disrupting both the structure and balance of multigene families. Note that these operators have been used by other researchers, but I took the liberty to change their names whenever the name previously given could cause confusion or does not reflect the GEP context of genes and MGFs. However, the correct references to the original names are given below.

Before proceeding with the description of their mechanisms, it is useful to compare their performances (Figure 1). The problem chosen to make this analysis is the TSP of section 4.1 with 19 cities using population sizes P of 100 and evolutionary times G of 200 generations. The 19 cities were arranged in a rectangle so that the shortest tour is 20. Therefore, the performance can be rigorously determined in terms of success rate, which is evaluated over 100 identical runs. As Figure 1 clearly demonstrates, the best operator is by far inversion, followed by gene deletion/insertion, whereas restricted permutation is extremely limited.

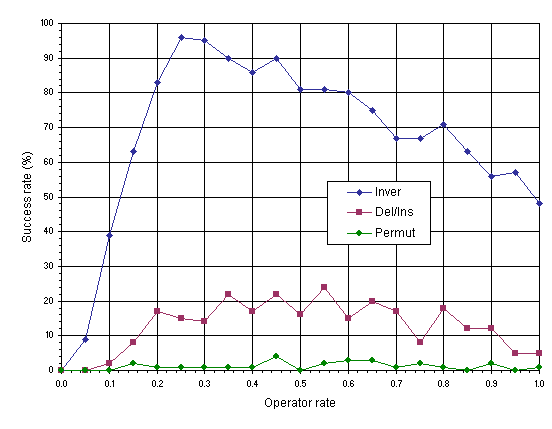
Figure 1. Comparison of inversion (Inver), gene deletion/insertion (Del/Ins), and restricted permutation (Permut) on the traveling salesperson problem with 19 cities. For this analysis P = 100 and G = 200. The success rate was evaluated over 100 identical runs.

Home | Contents | Previous | Next