As stated previously, the chromosomal organization used to solve combinatorial problems is very simple and consists of multigenic chromosomes composed of one-element genes, where each gene codes for a one-element expression tree (ET)
(Ferreira 2001). Furthermore, one-element genes may be organized in multigene families (MGFs), in which a particular class of terminals or tasks is gathered. Such chromosomes composed of MGFs are very useful to evolve solutions to combinatorial problems, as different classes of terminals/items can be included in each MGF. For instance, the different cities in the traveling salesperson problem may be encoded in a multigene family, where each gene codes for a city. Consider the simple chromosome below, composed of one MGF with nine members:
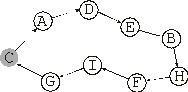
where each element represents a city. In this case, the expression of this chromosome consists of the spatial organization of the one-element ETs, for instance, the following tour for the traveling salesperson problem (the starting and finishing point is in gray):
For optimization problems with N classes of terminals, multigenic chromosomes composed of
N multigene families are used. For instance, the chromosome below composed of two MGFs with six
members each, was designed to evolve solutions to the simple task assignment problem of
section 4.2 (multigene families have different shades):
|
012345012345
632451EDFCBA |
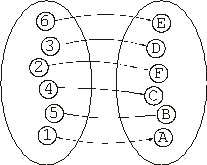
Its expression consists of the orderly interaction of the members of each MGF with one another as shown below:
|

