|
We have already met two different domains in GEP genes:
the head and the tail. And now another one – the Dc domain – will be
introduced. This domain was especially designed to handle random
numerical constants and consists of an extremely elegant, efficient,
and original way of dealing with them.
As an example, Genetic Programming handles random numerical
constants by using a special terminal named “ephemeral random
constant” (Koza 1992). For each
ephemeral random constant used in the trees of the initial
population, a random number of a special data type in a specified
range is generated. Then these random constants are moved around
from tree to tree by the crossover operator. Note, however, that
with this method no new constants are created during evolution.
Gene Expression Programming handles random numerical constants
differently (Ferreira 2001). GEP uses
an extra terminal “?” and an extra domain Dc composed of the symbols
chosen to represent the random constants. The values of each random
constant, though, are only assigned during gene expression. Thus,
for each gene, the initial random constants are generated during the
creation of the initial population and kept in an array. However, a
special operator is used to introduce genetic variation in the
available pool of random constants by mutating the random constants
directly. In addition, the usual operators of GEP (mutation,
inversion, transposition, and recombination), plus a Dc-specific
transposition and a Dc-specific inversion, guarantee the effective
circulation of the random constants in the population. Indeed, with
this scheme of constants’ manipulation, the appropriate diversity of
numerical constants is generated at the beginning of a run and
maintained easily afterwards by the genetic operators. Let’s take
then a closer look at the structural organization of this extra
domain and how it interacts with the sub-ET encoded in the head/tail
structure.
Structurally, the Dc comes after the tail, has a length equal to
t, and is composed of the symbols used to represent the random
constants. Therefore, another region with defined boundaries and its
own alphabet is created in the gene.
Consider the single-gene chromosome with an h = 8 (the Dc is
shown in blue):
|
01234567890123456789012345 |
|
|
*-Q*Q*?+?ba?babba238024198 |
(10) |
where the terminal “?” represents the random constants.
The expression of this kind of chromosome is done exactly as before,
obtaining:
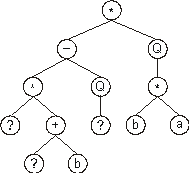
Then the ?’s in the expression tree are replaced from left
to right and from top to bottom by the symbols (numerals, for
simplicity) in Dc, obtaining:
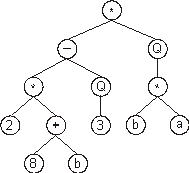
The random constants corresponding to these symbols are
kept in an array and, for simplicity, the number represented by the
numeral indicates the order in the array. For instance, for the
following array of 10 elements:
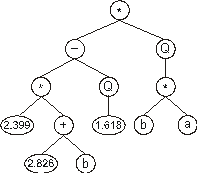
|
A = {1.095, 1.816, 2.399, 1.618, 0.725, 1.997,
0.094, 2.998, 2.826, 2.057} |
the chromosome (10) above gives:
This type of domain was used to great advantage not only
in symbolic regression but also in parameter optimization and
polynomial induction (Ferreira 2002a).
But this elegant structure can also be used to evolve the weights
and thresholds of evolvable neural networks (Ferreira
2004b) and to encode decision trees with numerical attributes
(unpublished material). And we will see here for the first time that
this kind of domain can also be used to create Automatically Defined
Functions with random numerical constants.
|


