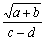The structural organization of GEP genes is better
understood in terms of open reading frames (ORFs). In biology, an
ORF or coding sequence of a gene begins with the start codon,
continues with the amino acid codons, and ends at a termination
codon. However, a gene is more than the respective ORF, with
sequences upstream of the start codon and sequences downstream of
the stop codon. Although in GEP the start site is always the first
position of a gene, the termination point does not always coincide
with the last position of a gene. Consequently, it is common for GEP
genes to have noncoding regions downstream of the termination point.
(For now we will not consider these noncoding regions, as they do
not interfere with expression.)
Consider, for example, the algebraic expression:
|
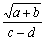 |
(1) |
It can also be represented as a diagram or ET:
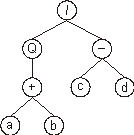
where “Q” represents the square root function.
This kind of diagram representation is in fact the phenotype of GEP
chromosomes. And the genotype can be easily inferred from the
phenotype as follows:
which is the straightforward reading of the ET from left to right
and from top to bottom (exactly as one reads a page of text). The
expression (2) is an open
reading frame, starting at “/” (position 0) and terminating at “b”
(position 7). These ORFs were named K-expressions from Karva
language.
Consider another ORF, the following K-expression:
|
0123456789 |
|
|
*//aQ*bddc |
(3) |
Its expression as an ET is also very simple and straightforward.
In order to express the ORF correctly, we must follow the rules
governing the spatial distribution of functions and terminals.
First, the start of a gene corresponds to the root of the expression
tree, and it occupies the topmost position (or first line) on the
tree. Second, in the next line, below each function, are placed as
many branch nodes as there are arguments to that function. Third,
from left to right, the nodes are filled consecutively with the next
elements of the K-expression. Fourth, the process is repeated until
a line containing only terminals is formed. In this case, the
following expression tree is formed:
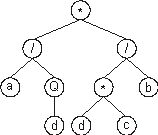
Looking at the structure of ORFs only, it is difficult or even
impossible to see the advantages of such a representation, except
perhaps for its simplicity and elegance. However, when open reading
frames are analyzed in the context of a gene, the advantages of this
representation become obvious. As I said before, GEP chromosomes
have fixed length, and they are composed of one or more genes of
equal length. Consequently, the length of a gene is also fixed.
Thus, in GEP, what changes is not the length of genes, but rather
the length of the ORF. Indeed, the length of an ORF may be equal to
or less than the length of the gene. In the first case, the
termination point coincides with the end of the gene, and in the
latter, the termination point is somewhere upstream of the end of
the gene. And this obviously means that GEP genes have, most of the
time, noncoding regions at their ends.
And what is the function of these noncoding regions at the end of
GEP genes? We will see that they are the essence of Gene Expression
Programming and evolvability, because they allow the modification of
the genome using all kinds of genetic operators without any kind of
restriction, always producing syntactically correct programs. Thus,
in GEP, the fundamental property of genotype/phenotype systems –
syntactic closure – is intrinsic, allowing the totally unconstrained
restructuring of the genotype and, consequently, an efficient
evolution.
In the next section we are going
to analyze the structural organization of GEP genes in order to
understand how they invariably code for syntactically correct
programs and why they allow the unconstrained application of
virtually any genetic operator.
|