The novelty of GEP genes resides in the fact that they are composed of a head and a tail. The head contains symbols that represent both functions and terminals, whereas the tail contains only terminals. For each problem, the length of the head h is chosen, whereas the length of the tail t is a function of h and the number of arguments n of the function with more arguments (also called maximum arity) and is evaluated by the equation:

Consider a gene for which the set of terminals T = {a, b} and the set of functions F = {Q, *, /, -, +}, thus giving n = 2. And if we chose an h = 10, then t = 10 (2 - 1) + 1 = 11 and the length of the gene g is 10 + 11 = 21. One such gene is shown below (the tail is shown in blue):

It codes for the following expression tree:

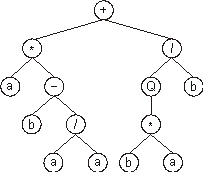
Note that, in this case, the open reading frame ends at position 13, whereas the gene ends at position 20.

Suppose now a mutation occurred at position 3, changing the “a” into “+”. Then the following gene is obtained:

And its expression gives:

In this case, the termination point shifts two positions to the right (position 15), enlarging and changing significantly the daughter tree.

Obviously the opposite might also happen, and the daughter tree might shrink. For example, consider again gene (5) above, and suppose a mutation occurred at position 2, changing the “/” into “b”:

And now its expression results in the following ET:

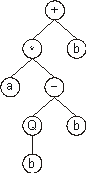
In this case, the ORF ends at position 7, shortening the original ET by six nodes.

So, despite their fixed length, the genes of Gene Expression Programming have the potential to code for expression trees of different sizes and shapes, where the simplest is composed of only one node (when the first element of a gene is a terminal) and the largest is composed of as many nodes as the length of the gene (when all the elements of the head are functions with maximum arity).

It is evident from the examples above, that any modification made in the genome, no matter how profound, always results in a structurally correct program. Consequently, the implementation of a powerful set of search operators, such as point mutation, inversion, transposition, and recombination, is a child’s play, making Gene Expression Programming the ideal playground for the discovery of the perfect solution using an economy of resources (see Ferreira 2001 and 2004a for a detailed description of the mechanisms and effects of the different genetic operators commonly used in Gene Expression Programming).