The task of the 11-bit boolean multiplexer is to decode a 3-bit binary address (000, 001, 010, 011, 100, 101, 110, 111) and return the value of the corresponding data register (d₀, d₁, d₂, d₃, d₄, d₅, d₆, d₇). Thus, the boolean 11-multiplexer is a function of 11 arguments: three, a₀ to a₂, determine the address, and eight, d₀ to d₇, determine the answer. As GEP uses single-character chromosomes, T = {a, b, c, 1, 2, 3, 4, 5, 6, 7, 8} which correspond, respectively, to {a₀, a₁, a₂, d₀, d₁, d₂, d₃, d₄, d₅, d₆, d₇}.

There are 2¹¹ = 2048 possible combinations for the 11 arguments of the boolean 11-multiplexer function. For this problem a random sampling of the 2048 combinations was used each generation as the fitness cases for evaluating fitness. The fitness cases were assembled by address, and for each address a sub-set of 20 random combinations was used each generation. Therefore, a total of 160 random fitness cases were used each generation as the adaptation environment. In this case, the fitness of a program is the number of fitness cases for which the boolean value returned is correct, plus a bonus of 180 fitness points for each sub-set of combinations solved correctly as a whole. Therefore, a total of 200 fitness points was attributed for each correctly decoded address, being the maximum fitness 1600. The idea was to make the algorithm decode one address at a time. And, in fact, the individuals learn to decode first one address, then another, until the last one (see Figure 17).

To solve this problem, multigenic chromosomes composed of 27 genes were used, each gene consisting of only one terminal. Thus, no functions were used to generate the chromosomes, although the sub-ETs were posttranslationally linked by IF.

The parameters used per run are shown in Table 2, column 5. The first correct solution in this experiment was found in generation 390 of run 1 (the characters are linked 3 by 3, forming an ET with depth 4, composed of 40 nodes, the first 14 nodes being IFs, and the remaining nodes, the chromosome characters; see K-expression (3.12) and Figure 5):

012345678901234567890123456
3652bb5bbba4c87c43bcca62a51

which is a universal solution for the 11-multiplexer. Figure 17 shows the progression of average fitness of the population and the fitness of the best individual for run 1 of the experiment summarized in Table 2, column 5.

As shown in the fifth column of Table 2, GEP solves the 11-multiplexer with a success rate of 0.57. It is worth noting that GP could not solve the 11-multiplexer with a population size 500 for 51 generations [18], and could only solve it using 4,000 individuals [9].

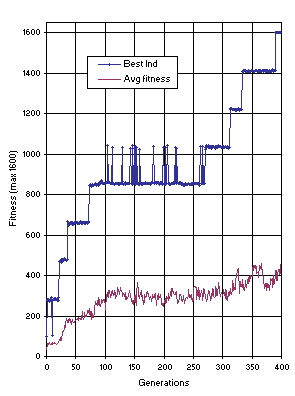
Figure 17. Progression of average fitness of the population and the fitness of the best individual for run 1 of the experiment summarized in Table 2, column 5 (11-multiplexer).