The gene deletion/insertion operator introduced in section 3.2 permits only the deletion/insertion of genes, i.e., the smallest sequence composed of only one element. Another operator can be easily implemented that deletes/inserts sequences of varied length. This operator was named “sequence deletion/insertion”, and corresponds to the “displacement mutation” operator in the classification proposed by Larrañaga et al. (1998). The deletion/insertion of sequences of different lengths might appear more advantageous than the deletion/insertion of genes, but experience shows the opposite (see Figure 2). In fact, this operator produces results which are even worse than the restricted permutation operator in the traveling salesperson problem with 19 cities (compare with Figure 1). In fact, an identical analysis done with this operator showed that the sequence deletion/insertion is incapable of solving the 19 cities TSP using population sizes of 100 individuals for 200 generations. Thus, an easier version of the TSP with 13 cities (with the cities also placed in a rectangle so that the shortest tour is 14) was chosen in order to make comparisons between gene deletion/insertion and sequence deletion/insertion (Figure 2). For this analysis, a population size of 100 individuals and an evolutionary time of 200 generations were used and the success rate was also evaluated over 100 identical runs.

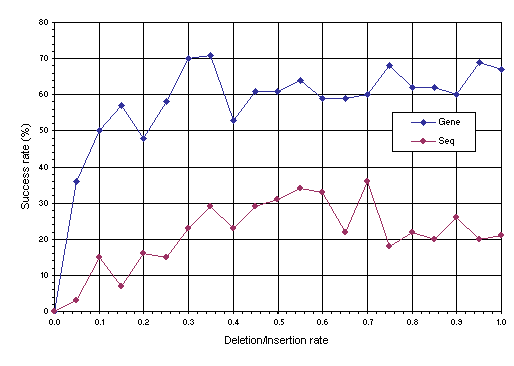
Figure 2. Comparison of gene deletion/insertion (Gene) with sequence deletion/insertion (Seq) on the traveling salesperson problem with 13 cities. For this analysis P = 100 and G = 200. The success rate was evaluated over 100 identical runs.

The other operator to be analyzed here is an extension to the restricted permutation operator of section 3.3. Recall that that kind of permutation operator exchanges only a pair of genes per chromosome, i.e., the restricted permutation rate p_rp is evaluated by p_rp = N_C/P, where N_C represents the number of chromosomes modified. A more generalized version of this operator can be easily implemented where a different number of genes in a chromosome can trade places with other genes according to a certain rate. More formally, the generalized permutation rate p_gp is evaluated by p_gp = N_G/(C_L.P), where N_G represents the number of genes modified and C_L the chromosome length. This operator was named “generalized permutation” and corresponds to the “exchange repeated mutation” operator in Larrañaga et al. (1998). Again, a more generalized permutation might appear more efficient than the restricted permutation described in section 3.3, but experience shows that restricted permutation is slightly better (see Figure 3). For instance, in the TSP with 19 cities (see Figure 1), this operator performed worse than restricted permutation and, in fact, was incapable of finding a perfect solution. The results obtained for the simpler version of the TSP with 13 cities are shown in Figure 3. In this analysis the restricted and generalized permutation are compared using populations of 100 individuals evolving for 200 generations, i.e., exactly the same values of P and G used to solve the much more complex TSP with 19 cities of Figure 1.

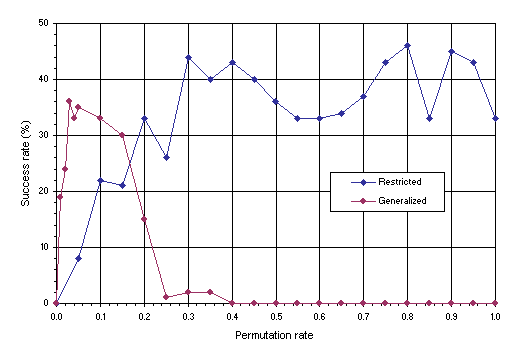
Figure 3. Comparison of restricted permutation with generalized permutation on the traveling salesperson problem with 13 cities. For this analysis P = 100 and G = 200. The success rate was evaluated over 100 identical runs.