The evolutionary dynamics of recombination show that all recombinational operators, from the most conservative (gene recombination) to the most disruptive (two-point recombination), display a homogenizing effect
(Figure 7.4). For obvious reasons, these recombination-specific dynamics are called
homogenizing dynamics. Note that, in all cases, the plot for average fitness closely accompanies the plot for best fitness and, given enough time, the plots tend to overlap and populations lose all genetic diversity (see, for instance, plots
c, g, and h). Note that this happens despite the recombination rate or the kind of recombinational operator involved and, in fact, by looking solely at these plots, not only is impossible to distinguish one kind of recombination from another but also more efficient systems from less efficient ones. Indeed, populations subjected to recombination alone become less and less diverse with time, becoming totally incapable of adaptation. Obviously, if populations converge to this stage before finding a good solution, they become irrevocably stuck in that point if no other, non-homogenizing operators are available. As the small success rates obtained for recombination emphasize (see
Figure 7.1), when populations evolve exclusively by recombination, most of the times they converge before finding a good solution. This shows that recombination should never be used as the only source of genetic variation if an efficient adaptation is what is desired.
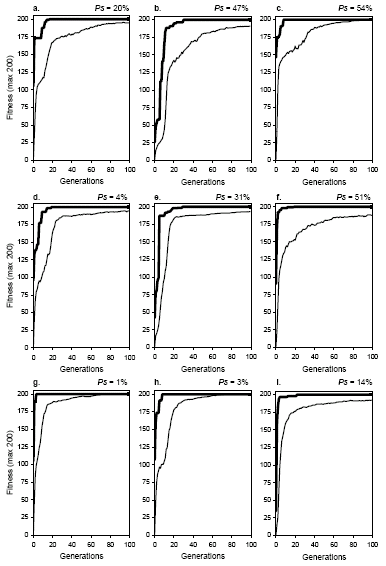
Figure 7.4. Evolutionary dynamics characteristic of populations undergoing two-point recombination (plots
a, b, and c), one-point recombination (plots d,
e, and f), and gene recombination (plots g, h, and
i). The success rate above each plot was evaluated in the experiment shown in
Figure 7.1. a) p2r = 0.3.
b) p2r = 0.6. c) p2r
= 1.0. d) p1r = 0.3. e) p1r = 0.6.
f) p1r = 1.0. g) pgr = 0.3.
h) pgr = 0.6. i) pgr
= 1.0. Note that all kinds of recombination generate the same type of homogenizing dynamics. Note also that these dynamics are very different from the dynamics of mutation and transposition (see Figures
7.2 and 7.3).
Note also that the oscillations on average fitness are less pronounced in homogenizing dynamics. Nevertheless, oscillations increase slightly with recombination rate showing that highly recombining populations are more resilient and will take more time before they become stagnant.
In summary, recombination is a homogenizing operator and, therefore, inappropriate to create genetic diversity; in the long run, populations exclusively subjected to recombination become stagnant. Consequently, recombination is removed from the center of the evolutionary storm and new roles must be proposed for this operator. For one thing, it can play an important role in the duplication of genes if it is combined with other genetic operators such as gene transposition. For another, it can play the role of a status quo agent, maintaining populations steady by permanently working at homogenizing their genetic makeup. Indeed, species are stable entities from their birth to their extinction (Eldredge and Gould
1972) and operators such as homologous recombination are fundamental to maintaining the status quo.
On the other hand, we also observed that the performance of a system not only changes dramatically with mutation rate but also that the performance peak is accessible to mutation alone. Therefore, mutation rates can be easily tuned so that systems could evolve with maximum efficiency. In fact, mutation rates are themselves tightly controlled and subjected to selection pressures in nature, another indication that mutation, and not recombination, is the center of the evolutionary storm.
And finally, we also observed that transposition operators display dynamics similar to those of mutation (i.e., non-homogenizing dynamics) and that populations undergoing transposition evolve significantly better than populations undergoing recombination alone, further emphasizing the unique, homogenizing effect of recombination.
|