We have already seen that all genetic operators contribute, directly or indirectly, to move the weights and thresholds around. And, in fact, this constant shuffling is more than sufficient to allow an effective evolution of GEP-NNs as the appropriate number of weights and thresholds is randomly created at the beginning of each run. However, we can also implement special mutation operators that replace the value of a particular weight or threshold by another.
These operators, called direct mutation of weights or thresholds, randomly select particular targets in the arrays where the weights or thresholds are kept, and randomly generate a new real-valued number. Consider for instance the array:
|
Wi,j = {-0.433, -1.823, 1.255, 0.028, -1.755, -0.036, -0.128,
-1.163, 1.806, 0.083} |
encoding the weights of gene j on chromosome i. Suppose a mutation occurred at position 7, changing the number -1.163 occupying that position by -0.494, giving:
|
Wi,j = {-0.433, -1.823, 1.255, 0.028, -1.755, -0.036, -0.128,
-0.494, 1.806, 0.083} |
The consequences of this kind of mutation are very diverse: they might be neutral in effect (for instance, when the gene itself is neutral; or when the weight or threshold has no expression on the sub-NN) or they might have manifold effects. The latter occurs whenever the weight or threshold modified happens to be used more than once in the expression of the sub-NN
(Figure 5.3).
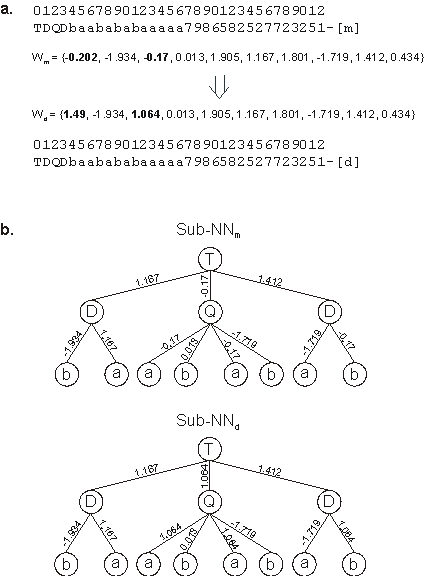
Figure 5.3. Illustration of direct mutation of weights. a) The mother and daughter chromosomes with their respective weights. In this case, weights at positions 0 and 2 were mutated. Note that the network architecture is the same for both mother and daughter.
b) The mother and daughter NNs encoded in the chromosomes. Note that the point mutation at position 2 (-0.17) has manifold effects as this weight appears four times in the neural network. Note also that a mutation in weights at positions 0, 4, 6, and 9 would have a neutral effect as these weights have no expression on the neural network.
Interestingly, this kind of mutation seems to have a very limited importance and better results are obtained when this operator is switched off. Indeed, the direct mutation of numerical constants in function finding problems produces identical results. Therefore, we can conclude that a well dimensioned initial diversity of numerical constants, be they the numerical constants of a mathematical expression or the weights or thresholds of a neural network, is more than sufficient to allow their evolutionary tuning. Typically, per gene, I use an array length of 10 weights for domain lengths equal to or less than 20. For larger domains we could increase the number of elements but most of the times an array of length 10 works very well.
|
