The objective of this section is to show how GEP can be used to model complex realities with high accuracy. The test function chosen is the following five parameter function:
|
|
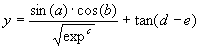
(4.5) |
where a, b, c, d, and e are the independent variables, and
exp is the irrational number 2.71828183.
Consider we were given a sampling of the numerical values from this function over 50 random points in the interval [0, 1] and we wanted to find a function fitting those values within 0.01% of the correct value. The fitness was evaluated by equation
(3.1b), and a selection range of 100% was chosen. Thus, for a set of 50 fitness cases,
fmax = 5000.
The set of 50 fitness cases used in this complex task could very well be unrepresentative of the problem domain, and the program evolved by GEP would be modeling a reality other than the reality of function
(4.5). To solve this dilemma, it is common to use a testing set with a reasonable amount of sample data. This data set is not used during evolution and therefore can be used to check the accuracy of the model and its generalizing capabilities. For this problem, and because it does not delay evolution, we can be generous and use a testing set of 200 random samples.
The domain of this problem suggests, besides the arithmetical functions, the use of
sqrt(x), exp(x), sin(x), cos(x) and tan(x) in the function set, which correspond in Karva notation, respectively, to “Q”, “E”, “S”, “C”, and “T”. Thus, for this problem, the function set consisted of
F = {+, -, *, /, Q, E, S, C, T}, and the set of terminals consisted obviously of the independent variables, giving
T = {a, b, c, d, e}.
For this problem, two-genic chromosomes encoding sub-ETs with a maximum of 25 nodes each were chosen. The sub-ETs were posttranslationally linked by addition. The parameters used per run are summarized in
Table 4.3.
Table 4.3
Settings for the five-parameter function problem.
| Number
of generations |
100 |
| Population
size |
500 |
| Number
of fitness cases |
50 |
| Function
set |
+
- * / Q E S C T |
| Terminal
set |
a b c
d e |
| Head
length |
12 |
| Number
of genes |
2 |
| Linking
function |
+ |
| Chromosome
length |
50 |
| Mutation
rate |
0.044 |
| One-point
recombination rate |
0.3 |
| Two-point
recombination rate |
0.3 |
| Gene
recombination rate |
0.1 |
| IS
transposition rate |
0.1 |
| IS
elements length |
1,2,3 |
| RIS
transposition rate |
0.1 |
| RIS
elements length |
1,2,3 |
| Gene
transposition rate |
0.1 |
| Selection
range |
100% |
| Precision |
0% |
Given the complexity of the problem, I used the software Automatic Problem Solver (APS) to model this function because it allows the easy optimization of intermediate solutions. Furthermore it also allows the easy checking of the evolved models against a testing set and the evaluation of standard statistical parameters such as the correlation coefficient R-square. In one run a very good solution with an R-square of 0.999964 evaluated over 200 points in the testing set was found:
|
01234567890123456789012340123456789012345678901234 |
|
|
*S*aCCQbSc+aabadedbadeecaT-deECd+/+Ccacdadddabceaa |
(4.6a) |
Mathematically, it corresponds to the following expression:
|
|
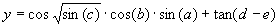
(4.6b) |
With APS we can convert automatically the evolved Karva program into a more conventional computer program. In this case, the model
(4.6a) above is automatically translated into the following C++ function:
double
APSCfunction(double d[ ])
{
double dblTemp = 0;
dblTemp += tan((d[3]-d[4]));
dblTemp += (sin(d[0])*(cos(sqrt(sin(((d[1]-d[1])+d[2]))))*cos(d[1])));
return dblTemp; |
|
|
} |
(4.6c) |
where d0 - d4 correspond, respectively, to
a - e. Note that three of the terms of this model match exactly the target function
(4.5). Note, however, that the term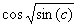 
was discovered by GEP as an excellent approximation to  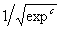. Indeed, as we will see again and again in this book, gene expression programming can be used to find very good solutions to problems of great complexity.
|