|
In this chapter:
The fundamental steps of the gene expression algorithm (GEA) are schematically represented in
Figure 3.1. The process begins with the random generation of the chromosomes of a certain number of individuals (the initial population). Then these chromosomes are expressed and the fitness of each individual is evaluated against a set of fitness cases (also called selection environment which, in fact, is the input to a problem). The individuals are then selected according to their fitness (their performance in that particular environment) to reproduce with modification, leaving progeny with new traits. These new individuals are, in their turn, subjected to the same developmental process: expression of the genomes, confrontation of the selection environment, selection, and reproduction with modification. The process is repeated for a certain number of generations or until a good solution has been found.
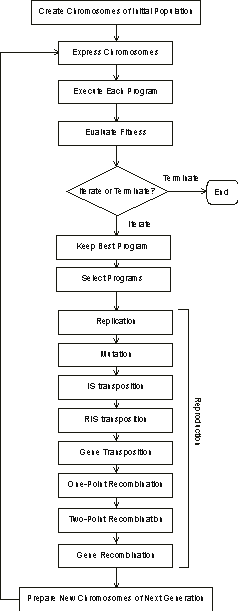
Figure 3.1. The flowchart of a gene expression algorithm.
In this chapter we will analyze with great detail all the fundamental steps of this algorithm, starting with the random generation of the chromosomes of the individuals of the initial population and finishing with reproduction. The goal consists not only of studying the logistics of the algorithm but also of understanding why and how populations of computer programs evolve, finding good solutions to particular problems. We have already seen that populations of entities, be they organisms or computer programs, evolve because individuals are reproduced with modification, giving rise to genetic diversity which is the raw material of evolution. This genetic diversity is the basis for selection and, therefore, plays a central role in evolution. Thus, we are going to analyze thoroughly the mechanisms and effects of all the agents of genetic diversity – the genetic operators. Each genetic operator is going to be used to solve the same simple problem so that entire populations could be fully analyzed and the power of each genetic operator could be completely understood. The problem used throughout this chapter to illustrate the internal workings of all the genetic operators is very simple and easy to understand and consists of the Boolean majority function of three arguments.
Furthermore, the chapter closes with the exhaustive analysis of a simple symbolic regression problem, taking us through all the steps necessary to apply GEP to solve a particular problem.
|
