|
The 6-bit multiplexer is a complex Boolean function of six activities. Its rule table is shown in
Table 3.
Table 3
Lookup table for the 6-multiplexer. The output bits are given in lexicographic order starting with 000000 and finishing with 111111.

In order to simplify the analysis, a rather compact chromosomal organization
was chosen and the “Q” function was not included in the function
set. Thus, for this problem,
F = {3U, 3D, 3T}, where “U” represents a function with connectivity
one;
T = {a, b, c, d, e, f}, representing the six arguments to the 6-multiplexer function; and
W = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, each taking values from the interval [-2, 2].
For the experiment summarized in the first column of Table
4, single-gene chromosomes were chosen so that the simulation of the 6-multiplexer function, a four modular function, went totally unbiased. One of the most parsimonious solutions
designed is shown in
Figure 6.
Table 4
Parameters for the 6-multiplexer problem.
| |
Unigenic
System |
Multigenic
System |
| Number
of runs |
100 |
100 |
| Number
of generations |
2000 |
2000 |
| Population
size |
50 |
50 |
| Number
of fitness cases |
64 (Table
3) |
64 (Table
3) |
| Function
set |
3U 3D
3T |
3U 3D
3T |
| Terminal
set |
a b c
d e f |
a b c
d e f |
| Linking
function |
-- |
O |
| Weights
array length |
10 |
10 |
| Weights
range |
[-2,
2] |
[-2,
2] |
| Head
length |
17 |
5 |
| Number
of genes |
1 |
4 |
| Chromosome
length |
103 |
124 |
| Mutation
rate |
0.044 |
0.044 |
| Intragenic
two-point recombination rate |
0.6 |
0.6 |
| Gene
recombination rate |
-- |
0.1 |
| Gene
transposition rate |
-- |
0.1 |
| IS
transposition rate |
0.1 |
0.1 |
| IS
elements length |
1,2,3 |
1,2,3 |
| RIS
transposition rate |
0.1 |
0.1 |
| RIS
elements length |
1,2,3 |
1,2,3 |
| Weights
mutation rate |
0.002 |
0.002 |
| Dw-specific
transposition rate |
0.1 |
0.1 |
| Dw-specific
IS elements length |
2,3,5 |
2,3,5 |
| Success
rate |
4% |
6% |
Obviously, we could explore the multigenic nature of GEP chromosomes and evolve multigenic neural networks. The solutions found are, however, structurally more constrained as we have to choose some kind of linking function
(Ferreira 2001) to link the sub-neural nets encoded by each gene. For this problem, the Boolean function OR was chosen to link the
sub-NNs. (If the mixing of OR with “U”, “D”, and “T” functions is confusing, think of OR as a function with connectivity two with a threshold and weights all equal to 1, and you have a neural net for the OR function.)
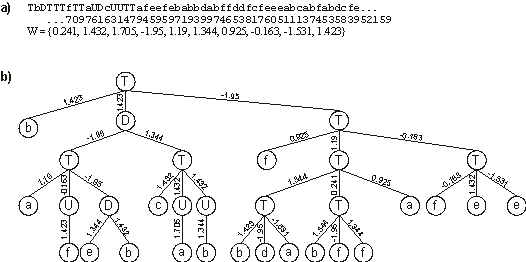
Figure 6. A perfect solution to the 6-multiplexer function discovered with GEP designed neural networks.
a) Its chromosome and corresponding array of weights. b) The fully expressed neural network encoded in the chromosome.
In the experiment summarized in the second column of Table
4, four genes posttranslationally linked by OR were used. The first solution found in this experiment is shown in
Figure 7. Note that some weights in genes 1 and 2 have identical values, and that the same happens for genes 3 and 4. This most probably means that these genes share a common ancestor.
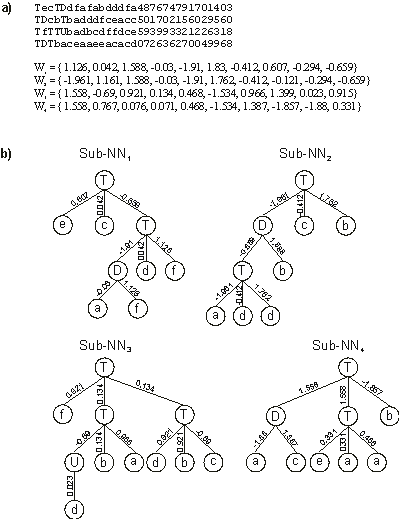
Figure 7. A perfect solution to the 6-multiplexer problem encoded in a four-genic chromosome.
a) Its chromosome with each gene shown separately. W1-W4 are the arrays containing the weights of each gene.
b) The sub-neural networks codified by each gene. In this perfect solution, the
sub-NNs are linked by OR.
|


