The comparison between the two approaches (with and without the facility to manipulate random constants) was made on three different problems. The first is a problem of sequence induction requiring integer constants. The
nth term N of the chosen sequence is given by the formula:
|
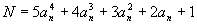
|
(3.2) |
where an consists of the nonnegative integers. This sequence was chosen because it can be exactly solved and therefore can provide an accurate measure of performance in terms of success rate.
The second is a problem of function finding requiring floating-point constants. In this case, the following “V” shaped function was chosen:
|
y = 4.251a2
+ ln(a2) + 7.243ea |
(3.3) |
where a is the independent variable and e is the irrational number 2.71828183. Problems of this kind cannot be exactly solved by evolutionary algorithms and, therefore, the performance of both approaches is compared in terms of average best-of-run fitness and average best-of-run R-square.
The third is the well-studied benchmark problem of predicting sunspots (Weigend et al.
1992). In this case, 100 observations of the Wolfer sunspots series were used
(Table 1) with an embedding dimension of 10 and a delay time of one. Again, the performance of both approaches is compared in terms of average best-of-run fitness and R-square.
Table 1
Wolfer sunspots series (read by rows).
| 101 |
82 |
66 |
35 |
31 |
7 |
20 |
92 |
| 154 |
125 |
85 |
68 |
38 |
23 |
10 |
24 |
| 83 |
132 |
131 |
118 |
90 |
67 |
60 |
47 |
| 41 |
21 |
16 |
6 |
4 |
7 |
14 |
34 |
| 45 |
43 |
48 |
42 |
28 |
10 |
8 |
2 |
| 0 |
1 |
5 |
12 |
14 |
35 |
46 |
41 |
| 30 |
24 |
16 |
7 |
4 |
2 |
8 |
17 |
| 36 |
50 |
62 |
67 |
71 |
48 |
28 |
8 |
| 13 |
57 |
122 |
138 |
103 |
86 |
63 |
37 |
| 24 |
11 |
15 |
40 |
62 |
98 |
124 |
96 |
| 66 |
64 |
54 |
39 |
21 |
7 |
4 |
23 |
| 55 |
94 |
96 |
77 |
59 |
44 |
47 |
30 |
| 16 |
7 |
37 |
74 |
|
|
|
|
|