In GEP, from the simplest individual to the most complex, the expression of the genetic information starts with translation, the transfer of information from a gene into an ET. We have already seen that translation results in the formation of sub-ETs with different sizes and shapes but, in most cases, the complete expression of the genetic information requires the interaction of these sub-ETs with one another. One of the most simple interactions is the linking of sub-ETs by a particular function. This process is similar to the assemblage of different protein subunits in a multi-subunit protein.
When the sub-ETs are algebraic or Boolean expressions, any algebraic or Boolean function with more than one argument can be used to link the sub-ETs in a final, multi-subunit ET. The functions most chosen are addition or multiplication for algebraic sub-ETs, and OR or IF for Boolean
sub-ETs.
Figure 2 illustrates the linking of three sub-ETs by addition.
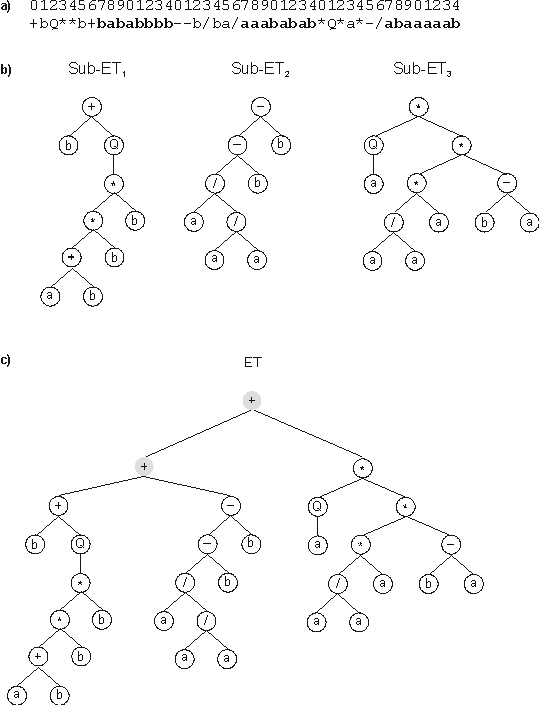
Figure 2. Expression of algebraic multigenic chromosomes as multi-subunit expression trees.
a) A three-genic chromosome with the tails shown in bold. b) The sub-ETs codified by each gene.
c) The result of posttranslational linking with addition. The linking functions are shown in gray.
Note that the final ET could be linearly encoded as the following K-expression:
| 012345678901234567890123456789012 |
|
|
++*+-Q*bQ-ba*-*/b/aba*ba/aa+baaab |
(2.9) |
However, to evolve solutions to complex problems, it is more effective the use of multigenic chromosomes, for they permit the modular construction of complex, hierarchical structures, where each gene codes for a small building block
(Ferreira 2001). These small building blocks are separated from each other, and thus can evolve independently. Furthermore, these multigenic systems are much more efficient than unigenic ones. Indeed, GEP is effectively a hierarchical invention system capable of discovering simple blocks and using them to form more complex structures.
Figure 3 shows another example of posttranslational interaction, where three Boolean sub-ETs are linked by the function
IF(x, y, z) (if x = 1, then return y; otherwise return
z).
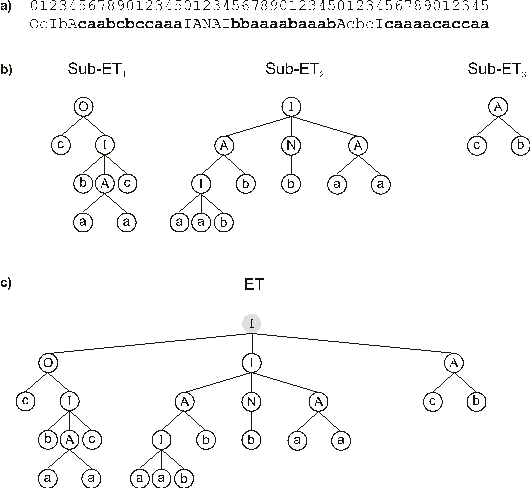
Figure 3. Expression of Boolean multigenic chromosomes as multi-subunit expression trees.
a) A three-genic chromosome with the tails shown in bold (‘N’ is a function of one argument and represents NOT; ‘A’ and ‘O’ are functions of two arguments and represent respectively AND and OR; ‘I’ is a function of three arguments and represents IF; the remaining symbols are terminals).
b) The sub-ETs codified by each gene. c) The result of posttranslational linking with IF. The linking function is shown in gray.
Again, the multi-subunit ET could be linearized into the following K-expression:
| 012345678901234567890123 |
|
|
IOIAcIANAcbbAcIbbaaaaaab |
(2.10) |
where ‘N’, ‘A’, ‘O’, and ‘I’ represent respectively the Boolean functions NOT, AND, OR and IF, taking ‘N’ one argument, ‘A’ and ‘O’ two, and ‘I’ three arguments.
So, for each problem, the type of linking function, as well as the number of genes and the length of each gene, are a priori chosen for each problem. While attempting to solve a problem, we can always start by using a single-gene chromosome and then proceed by increasing the length of the head. If it becomes very large, we can increase the number of genes and obviously choose a function to link the sub-ETs. We can start with addition for algebraic expressions or OR for Boolean expressions, but in some cases another linking function might be more appropriate (like multiplication or IF, for instance). The idea, of course, is to find a good solution, and GEP provides the means of finding one very efficiently.
|

