|
The aim of this section is to study a successful run in its entirety in order to understand how populations of GEP individuals evolve towards a perfect or good solution.
In symbolic regression or function finding the goal is to find an expression that satisfactorily explains the dependent variable. The input into the system is a set of fitness cases in the form
(a(i,0), a(i,1), ...,
a(i,n-1), yi) where
a(i,0) - a(i,n-1) are the independent variables and
yi is the dependent variable. The set of fitness cases consists of the adaptation environment where solutions adapt, discovering, in the process, solutions to problems.
In the example of this section, a simple test function was chosen, being therefore the fitness cases computer generated. Thus, in this case, we know exactly which function we are aiming at (remember, however, that in real-world problems the function is obviously unknown). So, suppose we are given a sampling of the numerical values from the curve:
over 10 randomly chosen points in the real interval [-10, +10] and we wanted to find a function fitting those values within a certain error. In this case, we are given a sample of data in the form of 10 pairs (ai,
yi), where ai is the value of the independent variable in the given interval and
yi is the respective value of the dependent variable
(ai values: -4.2605, -2.0437, -9.8317, -8.6491, 0.7328, -3.6101, 2.7429, -1.8999, -4.8852, 7.3998; the corresponding
yi values can be easily evaluated). These 10 pairs are the fitness cases (the input) that will be used as the adaptation environment. The fitness of a particular program will depend on how well it performs in this environment.
There are five major steps in preparing to use gene expression programming, and the first is to choose the fitness function. For this problem we could measure the fitness
fi of an individual program i by the following expression:
|
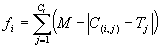
|
(4.2) |
where M is the range of selection, C(i,j) the value returned by the individual chromosome
i for fitness case j (out of Ct fitness cases) and
Tj is the target value for fitness case j. If,
for all j, |C(i,j) -
Tj| (the precision) less than or equal to 0.01, then the precision is equal to zero, and
fi = fmax = Ct*M.
For this problem, we will use an
M = 100 and, therefore, fmax = 1000. The advantage of this kind of fitness function is that the system can find the optimal solution for itself.
The second major step consists in choosing the set of terminals T and the set of functions
F to create the chromosomes. In this problem, the terminal set consists obviously of the independent variable, i.e.,
T = {a}. The choice of the appropriate function set is not so obvious, but a good guess can always be done in order to include all the necessary functions. In this case, to make things simple, we will use the four basic arithmetic operators. Thus,
F = {+, -, *, /}.
The third major step is to choose the chromosomal architecture, i.e., the length of the head and the number of genes. In this problem we will use an
h = 6 and three genes per chromosome.
The fourth major step in preparing to use gene expression programming is to choose the linking function. In this case we will link the sub-ETs by addition.
And finally, the fifth major step is to choose the set of genetic operators that cause variation and their rates. In this case we will use a combination of all genetic operators (mutation at
pm = 0.051; IS and RIS transposition at rates of 0.1 and three transposons of length 1, 2, and 3; one-point and two-point recombination at rates of 0.3; gene transposition and gene recombination both at rates of 0.1).
To solve this problem, I chose an evolutionary time of 50 generations and a small population of 20 individuals in order to simplify the analysis of the evolutionary process and not fill this text with pages of encoded individuals. However, one of the advantages of GEP is that it is capable of solving relatively complex problems using small population sizes and, thanks to the compact Karva notation, it is possible to fully analyze the evolutionary history of a run.
To show evolution at work, I chose a successful run in which a perfect solution was found in generation 3. The initial population of this run, together with the fitness of each individual, is shown below:
|
Generation N: 0
012345678901201234567890120123456789012
+**/*/aaaaaaa/+a/a*aaaaaaa/a-*a+aaaaaaa-[ 0] = 577.3946
--aa++aaaaaaa+-/a*/aaaaaaa/--a-aaaaaaaa-[ 1] = 0
/***/+aaaaaaa*+/+-aaaaaaaa++aa/aaaaaaaa-[ 2] = 463.6533
-/+/++aaaaaaa+-//+/aaaaaaa+-/a/*aaaaaaa-[ 3] = 546.4241
++a/*aaaaaaaa+-+a*-aaaaaaa-a/-*aaaaaaaa-[ 4] = 460.8625
*+*a-*aaaaaaa*a/aa/aaaaaaa//+*a/aaaaaaa-[ 5] = 353.2168
*/**+aaaaaaaa+a/**+aaaaaaa----+/aaaaaaa-[ 6] = 492.6827
*aa-+-aaaaaaa+a/-+/aaaaaaa***/-*aaaaaaa-[ 7] = 560.9289
+/-*//aaaaaaa*+*//+aaaaaaa-/**+*aaaaaaa-[ 8] = 363.4358
--a+*/aaaaaaa+a++--aaaaaaa+a+aa+aaaaaaa-[ 9] = 386.7576
+-*-**aaaaaaa*/-+**aaaaaaa*+--++aaaaaaa-[10] = 380.6484
/a-**/aaaaaaa/-a/a/aaaaaaa+/a/-*aaaaaaa-[11] = 0
+--+//aaaaaaa+*+/*-aaaaaaa/*-a-+aaaaaaa-[12] = 551.2066
-a/+a/aaaaaaa*/--/aaaaaaaa*-+/a+aaaaaaa-[13] = 308.1296
/+/-+-aaaaaaa+-a/aaaaaaaaa**+-*-aaaaaaa-[14] = 0
//-*+/aaaaaaa//*a+aaaaaaaa/a++a*aaaaaaa-[15] = 489.5392
*a-a*-aaaaaaa+*+-a/aaaaaaa*/*aa*aaaaaaa-[16] = 399.2122
-a++*/aaaaaaa+/aa-*aaaaaaa---/**aaaaaaa-[17] = 317.6631
--a/*aaaaaaaa++*+-aaaaaaaa+-/*+-aaaaaaa-[18] = 597.8777
*+++-/aaaaaaa/--///aaaaaaa+-+aaaaaaaaaa-[19] = 661.5933
|
Note that three of the 20 individuals are nonviable and thus have fitness 0. The best of generation, chromosome 19, has fitness 661.5933. Note that the second gene of this individual returns 0 and, therefore, might be considered a pseudogene. The descendants of the individuals of the initial population are shown below:
|
Generation N: 1
012345678901201234567890120123456789012
*+++-/aaaaaaa/--///aaaaaaa+-+aaaaaaaaaa-[ 0] = 661.5933
-a++*/aaaaaaa+//a--aaaaaaa---/**aaaaaaa-[ 1] = 0
+-*-**aaaaaaa*/-+**aaaaaaa*+--++aaaaaaa-[ 2] = 380.6484
+-*-**aaaaaaa*/-+**aaaaaaa*/*a**aaaaaaa-[ 3] = 356.9471
+-+aaaaaaaaaa*+++-/aaaaaaa/--///aaaaaaa-[ 4] = 661.5933
*aa-+-aaaaaaa+a/++/aaaaaaa***+-*aaaaaaa-[ 5] = 567.9289
*a-a*-aaaaaaa+/*-a/aaaaaaa*+-*++aaaaaaa-[ 6] = 449.802
*aa-+-aaaaaaa+a/-+/aaaaaaa*+--++aaaaaaa-[ 7] = 961.8512
/***/+aaaaaaa*+/+-aaaaaaaa-a/-*aaaaaaaa-[ 8] = 470.5862
+--+//aaaaaaa+*+/*-aaaaaaa/*-a-+aaaaaaa-[ 9] = 551.2066
*+++-/aaaaaaa-//--/aaaaaaa+-+aaaaaaaaaa-[10] = 0
--+a*-aaaaaaa++a/*aaaaaaaa-a/-*aaaaaaaa-[11] = 487.3099
-a++*/aaaaaaa+/aa-*aaaaaaa---/**aaaaaaa-[12] = 317.6631
++a/*aaaaaaaa+-+a*-aaaaaaa++aa/aaaaaaaa-[13] = 451.464
+--+/-aaaaaaa+a/**+aaaaaaa----+/aaaaaaa-[14] = 493.5336
*/-a++aaaaaaa+/aa-*aaaaaaa---/**aaaaaaa-[15] = 356.4241
+/-*//aaaaaaa*+a//+aaaaaaa-/+*+*aaaaaaa-[16] = 493.9218
*/**+aaaaaaaa+*+/*aaaaaaaa***/-*aaaaaaa-[17] = 448.4805
+-*-**aaaaaaa*/-+**aaaaaaa*+--++aaaaaaa-[18] = 380.6484
++a/*aaaaaaaa+-+a*+aaaaaaa--/-*aaaaaaaa-[19] = 380.8585
|
Note that chromosome 0 is the clone of the best individual of the previous generation. In this generation, a new individual was created, chromosome 7, considerably better than the best individual of the initial population. The descendants of the individuals of this generation are shown below:
|
Generation N: 2
012345678901201234567890120123456789012
*aa-+-aaaaaaa+a/-+/aaaaaaa*+--++aaaaaaa-[ 0] = 961.8512
*/**+aaaaaaaa*/-+**aaaaaaa***/-*aaaaaaa-[ 1] = 446.2061
+-*-**aaaaaaa*+a//-aaaaaaa-/+*+*aaaaaaa-[ 2] = 323.1036
+--+//aaaaaaa+*+/*-aaaaaaa/*-*-+aaaaaaa-[ 3] = 551.2066
*aa-+-aaaaaaa+a/++/aaaaaaa***+-*aaaaaaa-[ 4] = 567.9289
++a/*aaaaaaaa*/-+-*aaaaaaa*+--++aaaaaaa-[ 5] = 0
+-*-**aaaaaaa+*+/*aaaaaaaa*/*a**aaaaaaa-[ 6] = 386.6484
++a/*aaaaaaaa+-+/*-aaaaaaa+aa++aaaaaaaa-[ 7] = 466.1533
+-*-a*aaaaaaa*/-+**aaaaaaa*a*a**aaaaaaa-[ 8] = 194.0452
/***/+aaaaaaa*+/+-aaaaaaaa-a--*aaaaaaaa-[ 9] = 541.4829
+-*-+*aaaaaaa+-+a*-aaaaaaa***/-*aaaaaaa-[10] = 346.2235
--*+*-aaaaaaa*aa-+-aaaaaaaaa/-+/aaaaaaa-[11] = 467.0862
*/-+**aaaaaaa+-*-*+aaaaaaa*/*a**aaaaaaa-[12] = 672.877
*aa+*/aaaaaaa+a/-+/aaaaaaa*+--++aaaaaaa-[13] = 961.8512
*+++/+aaaaaaa*++/+-aaaaaaa-a/-*aaaaaaaa-[14] = 395.858
/***-/aaaaaaa/--///aaaaaaa+-+a-aaaaaaaa-[15] = 467.0862
*aa-+-aaaaaaa+a/++/aaaaaaa***+-*aaaaaaa-[16] = 567.9289
+-+aaaaaaaaaa*+++-/aaaaaaa/--///aaaaaaa-[17] = 661.5933
+/-*//aaaaaaa*/a+**aaaaaaa*+--++aaaaaaa-[18] = 903.8886
*/**+aaaaaaaa+*+/*aaaaaaaa+/aa/aaaaaaaa-[19] = 423.885
|
Note that none of the descendants surpassed the best individual of the previous generation. And finally, in the next generation, an individual with maximum fitness was created:
|
Generation N: 3
012345678901201234567890120123456789012
*aa+*/aaaaaaa+a/-+/aaaaaaa*+--++aaaaaaa-[ 0] = 961.8512
*aa-+-aaaaaaa+a/-+/aaaaaaa/--///aaaaaaa-[ 1] = 560.9289
*aa-+-aaaaaaa-++/+-aaaaaaa-a/-*aaaaaaaa-[ 2] = 558.2066
*+++/+aaaaaaa*+a/-+aaaaaaa++--++aaaaaaa-[ 3] = 569.0469
/+++/+aaaaaaa*++/+-aaaaaaa-a/-*aaaaaaaa-[ 4] = 699.5153
+-+aa/aaaaaaa++++-/aaaaaaa***+-*aaaaaaa-[ 5] = 466.1533
*aa-+-aaaaaaaaa--**aaaaaaa*+--++aaaaaaa-[ 6] = 957.9443
--++*-aaaaaaa*a+/*-aaaaaaa+aa++aaaaaaaa-[ 7] = 337.7807
*aaa*/aaaaaaa+a+-+/aaaaaaa*+-/++aaaaaaa-[ 8] = 953.9443
/***/-aaaaaaa*+/+-aaaaaaaa-a--*aaaaaaaa-[ 9] = 0
*aa-+-aaaaaaa+a/-+/aaaaaaa*/--++aaaaaaa-[10] = 560.9289
*aa-+-aaaaaaa+a/++/aaaaaaa/--///aaaaaaa-[11] = 567.9289
+-+a-aaaaaaaa/***-/aaaaaaa*+--++aaaaaaa-[12] = 676.0663
+/**//aaaaaaa*/a+**aaaaaaa*+--++aaaaaaa-[13] = 1000
*/-+**aaaaaaa+-*-*+aaaaaaa*/*a**aaaaaaa-[14] = 672.877
/***/+aaaaaaa/+*+/+aaaaaaa-a*/--aaaaaaa-[15] = 498.3734
+/-*//aaaaaaa*/a+-*aaaaaaa*+--++aaaaaaa-[16] = 0
--*+--aaaaaaa*/a-+-aaaaaaa/a/-+/aaaaaaa-[17] = 506.1233
++a/*aaaaaaaa+-a-+-aaaaaaa-a*-+/aaaaaaa-[18] = 815.7772
*+a//-aaaaaaa+a/-+/aaaaaaa-/+*+*aaaaaaa-[19] = 412.5237
|
Note that this chromosome is a descendant, via mutation, of chromosome 18 of the previous generation: their chromosomes differ only in one position (the ‘-’ at position 2 of gene 1 was replaced by ‘*’). The expression of this chromosome shows that it codes for a perfect solution, the test function
(4.1).
|