GEP chromosomes are usually composed of more than one gene of equal length. For each problem or run, the number of genes, as well as the length of the head, are a priori chosen. Each gene codes for a sub-ET and the sub-ETs interact with one another forming a more complex multi-subunit ET.

Consider, for example, the following chromosome with length 45, composed of three genes (the tails are shown in blue):

It has three ORFs, and each ORF codes for a sub-ET (Figure 1). Position zero marks the start of each gene. The end of each ORF, though, is only evident upon construction of the respective sub-ET. As shown in Figure 1, the first ORF ends at position 8 (sub-ET₁); the second ORF ends at position 2 (sub-ET₂); and the last ORF ends at position 10 (sub-ET₃). Thus, GEP chromosomes contain several ORFs, each ORF coding for a structurally and functionally unique sub-ET. Depending on the problem at hand, these sub-ETs may be selected individually according to their respective fitness (for example, in problems with multiple outputs), or they may form a more complex, multi-subunit ET where individual sub-ETs interact with one another by a particular kind of posttranslational interaction or linking. For instance, algebraic sub-ETs can be linked by addition or multiplication whereas Boolean sub-ETs can be linked by OR, AND or if(x,y,z).

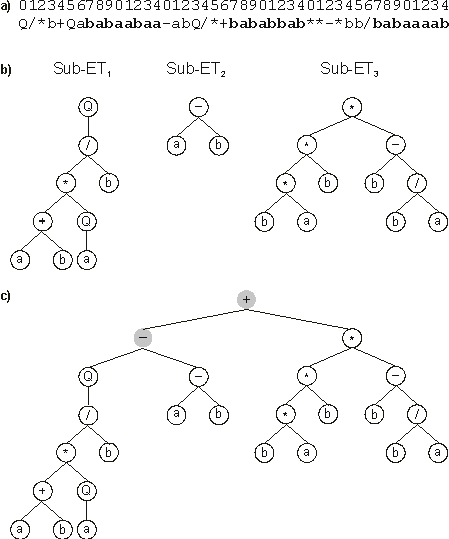
Figure 1. Expression of GEP genes as sub-ETs. a) A three-genic chromosome with the tails shown in bold. Position zero marks the start of each gene. b) The sub-ETs codified by each gene. c) The result of posttranlational linking with addition. The linking functions are shown in gray.

The linking of three sub-ETs by addition is illustrated in Figure 1, c. Note that the final ET could be linearly encoded as the following K-expression:

However, to evolve solutions to complex problems, it is more effective the use of multigenic chromosomes, for they permit the modular construction of complex, hierarchical structures, where each gene codes for a small building block. These small building blocks are separated from each other, and thus can evolve independently. Furthermore, these multigenic systems are much more efficient than unigenic ones. Indeed, GEP is a highly efficient hierarchical invention system capable of discovering simple blocks and using them to form more complex structures.

So, for each problem, the type of linking function, as well as the number of genes and the length of each gene, are a priori chosen. While attempting to solve a problem, we can always start by using a single-gene chromosome and then proceed by increasing the length of the head. If it becomes very large, we can increase the number of genes and obviously choose a function to link the sub-ETs. We can start with addition for algebraic expressions or OR for Boolean expressions, but in some cases another linking function might be more appropriate (like multiplication or IF, for instance). The idea, of course, is to find a good solution, and GEP provides the means of finding one very efficiently.