The sextic polynomial of this section x6-2x4+x2
was chosen by Koza (Koza 1994)
because of its potentially exploitable regularity and modularity,
easily guessed by its factorization:
|
x6-2x4+x2
= x2(x-1)2(x+1)2 |
(14) |
For this problem, the basic parameters common to both GEP and GP,
irrespective of the presence or absence of ADFs, were kept exactly
the same as those used by Koza. Thus, a set of 50 random fitness
cases chosen from the interval [-1.0, +1.0] was used; and a very
simple function set, composed only of the four arithmetic operators
F = {+, -, *, /} was used. As for random numerical constants, we
will see that their use in this problem is not crucial for the
evolution of perfect solutions. Nonetheless, evolution still goes
smoothly if integer constants are used and, therefore, one can
illustrate the role random constants play and how they are
integrated in Automatically Defined Functions by choosing integer
random constants. So, when used, integer random constants are chosen
from the interval [0, 3].
The fitness function used to evaluate the performance of each
evolved program is based on the relative error and explores the idea
of a selection range and a precision. The selection range is used as
a limit for selection to operate, above which the performance of a
program on a particular fitness case contributes nothing to its
fitness. And the precision is the limit for improvement, as it
allows the fine-tuning of the evolved solutions as accurately as
necessary.
Mathematically, the fitness fi of an individual
program i is expressed by the equation:
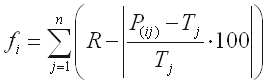 |
(15) |
where R is the selection range, P(ij)
the value predicted by the individual program i for fitness
case j (out of n fitness cases) and Tj
is the target value for fitness case j. Note that the
absolute value term corresponds to the relative error. This term is
what is called the precision and if the error is lower than or equal
to the precision then the error becomes zero. Thus, for a perfect
fit, the absolute value term is zero and fi = fmax
= nR. In all the experiments of this work we are going to use
a selection range of 100 and a precision of 0.01, thus giving for
the set of 50 fitness cases fmax = 5,000. It is
worth pointing out that these conditions, especially the precision
of 0.01, guarantee that all perfect solutions are indeed perfect and
match exactly the target function (14). This is
important to keep in mind since the performance of the different
systems will be compared in terms of success rate.
|