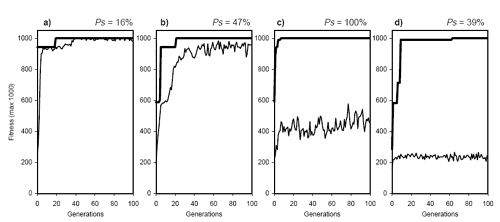
Figure 2. A gallery of evolutionary dynamics found in populations evolving by mutation. The success rate above each plot was determined in the experiment shown in Figure 1. a) Moderately Innovative dynamics, p_m = 0.001. b) Healthy But Weak dynamics, p_m = 0.005. c) Healthy And Strong dynamics, p_m = 0.1. d) Totally Chaotic dynamics, p_m = 1.0.


In the second dynamics, p_m = 0.005, we observe that, although closely accompanying the plot for best fitness, the plot for average fitness never touches the best fitness. Moreover, the oscillatory pattern on average fitness characteristic of GEP populations [3], is already evident even for such small variation rates. As shown in plot b of Figure 2, the success rate is in this case 47%. It can be said that, although adaptively healthy, the system is not very efficient. These systems are called Healthy But Weak. Note that the success rate increases progressively with the mutation rate until it reaches a plateau around p_m = 0.1 and, in terms of dynamics, this is reflected in a more pronounced oscillatory pattern in average fitness and an increase in the gap between both plots. Indeed, around p_m = 0.1 (Figure 2, plot c), the system is at its best with a success rate of 100%. These populations are called Healthy And Strong. Note that the gap between best and average fitness is considerably wider than in plots a and b, and the capacity to evolve is also higher. Obviously, all populations evolving with maximum performance (approximately from p_m= 0.033 to p_m = 0.20) have dynamics of the type Healthy And Strong.

The last dynamics of Figure 2, p_m = 1.0, is an example of Totally Chaotic systems. Note that, despite elitism, this dynamics is completely chaotic, for elitism is insignificant as each generation a totally random population is generated. Note also the less pronounced oscillatory pattern in average fitness and that the gap between average and best fitness is now maximal.