In GEP, the genome or chromosome consists of a linear, symbolic string of fixed length composed of one or more genes. As will next be shown, despite their fixed length, GEP chromosomes code for ETs with different sizes and shapes.
The structural organization of GEP genes is better understood in terms of open reading frames (ORFs). In biology, an ORF or coding sequence of a gene begins with the start codon, continues with the amino acid codons, and ends at a termination codon. However, a gene is more than the respective ORF, with sequences upstream of the start codon and sequences downstream of the stop codon. Although in GEP the start site is always the first position of a gene, the termination point does not always coincide with the gene last position. It is common for GEP genes to have non-coding regions downstream of the termination point. (For now these non-coding regions will not be considered because they do not interfere with the product of expression.)
Consider, for example, the algebraic expression:
|
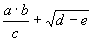
|
(2.1) |
It can also be represented as a diagram or ET:
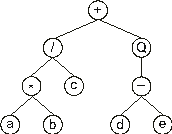
where Q represents the square root function.
This kind of diagram representation is in fact the phenotype of GEP chromosomes, where the genotype is easily inferred from the phenotype as follows:
|
0123456789 |
|
|
+/Q*c-abde |
(2.2) |
which is the straightforward reading of the ET from left to right and from top to bottom (exactly as we read a page of text). The expression
(2.2) is an ORF, starting at + (position 0) and terminating at e (position 9). These ORFs are called K-expressions (from Karva notation).
Consider another ORF, the following K-expression:
|
012345678901 |
|
|
*-/Qb+b+aaab |
(2.3) |
Its expression as an ET is also very simple and straightforward. To express correctly the ORF, the rules governing the spatial distribution of functions and terminals must be followed. The start position (position 0) in the ORF corresponds to the root of the ET. Then, below each function are attached as many branches as there are arguments to that function. The assemblage is complete when a baseline composed only of terminals (the variables or constants used in a problem) is formed. So, for the K-expression
(2.3) above, the following ET is formed:
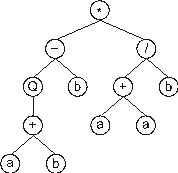
Looking at the structure of GEP ORFs only, it is difficult or even impossible to see the advantages of such a representation, except perhaps for its simplicity and elegance. However, when ORFs are analyzed in the context of a gene, the advantages of this representation become obvious. As stated previously, GEP chromosomes have fixed length, and they are composed of one or more genes of equal length. Therefore the length of a gene is also fixed. Thus, in GEP, what varies is not the length of genes but the length of the ORFs. Indeed, the length of an ORF may be equal to or less than the length of the gene. In the first case, the termination point coincides with the end of the gene and, in the latter, the termination point is somewhere upstream of the end of the gene.
In summary, GEP genes usually contain non-coding regions downstream of the termination point and, because of this apparently trivial fact, the genome of GEP individuals can be easily modified using any genetic operator. This means that, for the first time in evolutionary computation, a truly functional genotype/phenotype systems is created in which the search space can be thoroughly explored by a myriad of genetic operators, among which the high-performing point mutation
[7, 8]. In fact, the chromosomal organization of GEP individuals allows the easy implementation of genetic operators which always produce valid structures and, therefore, no repair whatsoever is necessary.
The section proceeds with the study of the structural organization of GEP genes in order to show how they invariably code for syntactically correct programs and why they allow the unconstrained application of any genetic operator.
|

