Another way of analyzing genetic neutrality in GEP, consists of increasing the number of genes. For that a compact, unigenic system capable of exactly solving the problem at hand is chosen as the starting point. Thus, the starting point for the function finding problem is a unigenic system with h = 6 (a chromosome length c of 13), and h = 14 (c = 14) for the sequence induction problem (see Figure 5).

As shown in Figure 6, the results obtained for multigenic systems further reinforce the importance of neutrality in evolution. Note that, in both experiments, the efficiency of the system increases dramatically with the introduction of a second gene and that compact unigenic systems are much less efficient than less compact, multigenic ones. For instance, in the function finding problem, the compact, unigenic system (c = 13) has a success rate of 2% whereas the success rate in the two-genic system (c = 26) is 94%. In the sequence induction problem, the success rate in the unigenic system (c = 29) is only 1%, whereas in the less compact two-genic system (c = 58) is 73%. Again, a plateau is observed where systems are most efficient, showing that a certain amount of redundancy is fundamental for evolution to occur efficiently. Indeed, it is intuitively understood that a certain room to experiment, not only by forming new building blocks but also by rejecting existing ones, is essential to come up with something new and useful. If there is no room to play, it is only costly (if ever) that one comes up with a good solution to the problem at hand. Note also that highly redundant systems are more efficient than extremely compact ones. For instance, the 10-genic system used in the function finding problem (c = 130), has a success rate of 61% compared to only 2% obtained with the most compact organization (c = 13). The same behavior can be observed in the sequence induction problem where the highly redundant 10-genic system (c = 290) performs slightly better than the extremely compact one (c = 29) (1% and 11%, respectively).

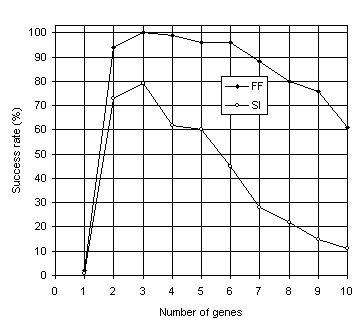
Fig. 6. Variation of success rate with number of genes for the function finding (FF) and sequence induction (SI) problems.


The comparison of Figures 5 and 6 also shows that multigenic systems are considerably better than unigenic ones. For instance, in the function finding problem, from two-genic to six-genic systems (corresponding to chromosome lengths c = 26 through c = 78) the success rates are in all cases above 94% and the best has a success rate of 100% (see Figure 6), whereas the best chromosome length in the unigenic system (c = 37 and h = 18) achieved only 76% (see Figure 5). The same phenomenon can be observed in the sequence induction problem in which from two-genic to five-genic systems (corresponding to c = 58 through c = 145) the success rates are above 60% and the best has a success rate of 79% (see Figure 6) whereas the best chromosome length in the unigenic system (c = 79 and h = 39) achieved only 43% (see Figure 5).

The structural analysis of compact solutions and less compact ones can also provide some insights into the role of redundancy in evolution. For instance, the following three perfect solutions to the sequence induction problem were obtained, respectively, for systems with only one gene, three, and five genes:

Note that not only does the total length of the non-coding regions increase from the most compact to the less compact but also does the number of neutral motifs. Specifically, the length of the non-coding region in the unigenic solution is only six and no neutral motifs are present; for the three-genic solution, the total length of the non-coding regions is 16 and three neutral motifs involving a total of 12 nodes can be counted; for the five-genic solution, the non-coding regions encompass already 66 elements and there are six neutral motifs involving a total of 31 nodes.