The task assignment problem (TAP) of this section is the toy problem chosen by
Tank and Hopfield (1987) in their
Scientific American article to illustrate the workings of Hopfield networks on combinatorial cost-optimization problems.
In TAP there are n tasks that must be accomplished by using only
n workers. Each worker performs better at some tasks and worse at others and obviously some workers are better than others at certain tasks. The goal is to minimize the total cost for accomplishing all tasks or, stated differently, to maximize the overall output of all the workers as a whole.
Suppose we had to shelve n book collections in a library using
n shelving assistants. Each assistant is familiar with the subject areas to varying degrees and shelves the collections accordingly. The input data or fitness cases in this task consist of the rates at which books are shelved per minute
(Figure 6.6).

Figure 6.6. The task assignment problem. Each assistant (1-6) should be assigned to one collection of books (A-F) based on the rates at which books are shelved per minute (fitness cases). Shaded squares show the best assignment with the largest sum of shelving rates, 44.
For this simple six-by-six problem there are already 6! = 720 possible assignments of assistants to book collections. The best solution has the highest sum of rates for the chosen assistants. For the particular set of fitness cases shown in
Figure 6.6, fmax = 44.
This kind of toy problem is very useful for comparing the performance of different algorithms and, here, the potentialities of inversion will be further tested in systems in which chromosomes composed of more than one multigene family are used. Indeed, the task assignment problem is solved very efficiently using only inversion as the source of genetic variation and two multigene families: one to encode the assistants (represented by 1-6) and another to encode the book collections (represented by A-F). Such a chromosome is shown below:
|
012345012345
652314DECFAB |
It contains two different MGFs, the first encoding the assistants and the second the book collections. And its expression gives:
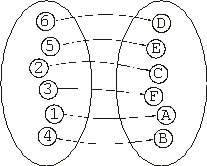
where the assignments are represented by the arrows. As you can see in
Figure 6.6, this individual has fi = 41.
For this problem, we are going to use small populations of 30 individuals and evolutionary times of 50 generations. The parameters used per run and the performance of the algorithm expressed in terms of success rate are shown in
Table 6.2.
Table 6.2
Parameters for the task assignment problem.
| Number
of runs |
100 |
| Number
of generations |
50 |
| Population
size |
30 |
| Number
of multigene families |
2 |
| Number
of genes per multigene family |
6 |
| Chromosome
length |
12 |
| Inversion
rate |
0.30 |
| Success
rate |
69% |
In the first successful run of this experiment, a solution with maximum fitness was discovered on generation 16:
|
012345012345
536241EDCFBA |
which corresponds to the best assignment of 44 (see also Figure
6.6 above):
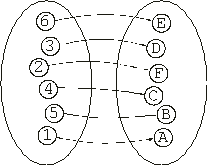
|


