In this section:
Obviously, combinatorial problems cannot be solved using the genetic operators of the basic gene expression algorithm without first modifying them. In these problems, the elements of a multigene family must all be present and cannot be represented more than once. Therefore, special mechanisms must be created in order to introduce genetic variation in the population. In this section, I will start by describing the three most efficient combinatorial-specific genetic operators: inversion, gene deletion/insertion, and restricted permutation, and finish by describing the less efficient ones: sequence deletion/insertion and generalized permutation. All these combinatorial-specific operators allow the introduction of genetic variation without disrupting the balance of multigene families and, therefore, always produce valid structures.
Before proceeding with the description of their mechanisms, it is useful to compare their performances
(Figure 6.2). The problem chosen to make this analysis is the traveling salesperson problem (TSP) of
section 6.3.1 with 19 cities using population sizes of 100 individuals and evolutionary times of 200 generations. As
Figure 6.2 clearly demonstrates, the best operator is by far inversion, followed by gene deletion/insertion, whereas restricted permutation is extremely inefficient.
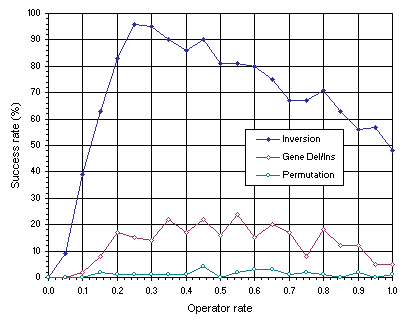
Figure 6.2. Comparison of inversion (Inversion), gene deletion/insertion (Gene Del/Ins), and restricted permutation (Permutation) on the traveling salesperson problem with 19 cities. For this analysis
P = 100 and G = 200. The success rate was evaluated over 100 identical runs.
|
