Figure 3.11. An initial population and its later descendants created, via mutation, to solve the Majority (a, b, c) function problem. The chromosomes encode sub-ETs linked by OR. Note that none of the later descendants are identical to their ancestors of generation 0. The perfect solution found in generation 6 (chromosome 1) and one of its putative ancestors (chromosome 0 of generation 5) are shown in blue. Note that chromosomes 1 and 3 of generation 5 are also good candidates to be the predecessors of the perfect solution. In both cases, two point mutations would have occurred during reproduction.

The most probable ancestors of this perfect solution are chromosomes 0, 1, and 3 of generation 5. In the first case, only one point mutation would have occurred during reproduction whereas two point mutations would have occurred in the last two cases. Figure 3.12 compares the ETs of one of these putative ancestors (chromosome 3) with the daughter ET, i.e., before and after mutation. In this case, two point mutations occurred during reproduction of chromosome 3: one changed the “N” at position 1 in gene 1 into “a”; and another changed the “a” at position 3 in gene 2 into “b”. Note that the first mutation changed significantly the sub-ET₁, shortening the original sub-ET in one node. Note also that, although the second mutation did not change the shape of the sub-ET, the expression encoded in this sub-ET is not the same.

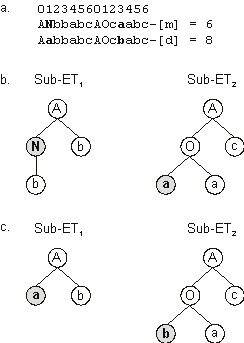
Figure 3.12. Illustration of mutation. a) The mother and daughter chromosomes with the mutation points shown in bold. b) The sub-ETs encoded by the mother chromosome (before mutation). c) The sub-ETs encoded by the daughter chromosome (after mutation). The mutation nodes are shown in gray. Note that the first mutation changed significantly the sub-ET₁, shortening the original sub-ET in one node.

Let us analyze more closely the populations shown in Figure 3.11. On the one hand, we can see that several mutations have a neutral effect. For instance, chromosome 7 of generation 6 is a descendant of chromosome 4 of generation 5. These chromosomes differ only at positions 1 and 4 in gene 2. The expression of these chromosomes gives identical ETs (Figure 3.13), as the mutations occurred downstream of the termination point of ORF₂. As we have seen, mutations occurring in the non-coding region of a gene have a neutral effect, as they have no expression in the “organism” itself.

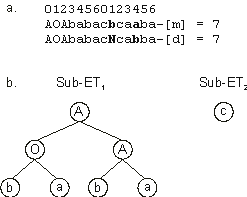
Figure 3.13. Illustration of neutral mutations. a) The mother and daughter chromosomes with the mutation points shown in bold. b) The sub-ETs encoded by both chromosomes. Note that the mutations shown in (a) have no expression in the final ET as they occurred downstream of the termination point.

On the other hand, we can see that, in GEP, mutations in the coding sequence of a gene have usually a very profound effect: most of the times they reshape the ET drastically. However, this capability to reshape profoundly the ET is fundamental for evolvability (see chapter 7 for a comparison of the genetic operators). Indeed, the results presented throughout this book clearly show that our too human wish to keep intact the small functional blocks and recombine them carefully (as is done in GP) is conservative and works poorly. Genotype/phenotype systems can find much more efficient ways of creating and manipulating their own building blocks. These building blocks are very different from the ones a mathematician would have chosen but, nonetheless, they work much more efficiently.

And finally, it is worth emphasizing that in GEP there are no constraints both in the kind of mutation and the number of mutations in a chromosome as, for all cases, the newly created individuals are syntactically correct programs. This important feature distinguishes GEP from all GP-style systems, where point mutations would have resulted most of the times in invalid programs. And an evolutionary algorithm unable to use this powerful operator is severely restricted, since mutation is the most important agent of genetic diversification (see chapter 7).