The simplest CA is a wrap-around array of N binary-state cells, where each cell is connected to
r neighbors from both sides. The state of each cell is updated by a defined rule. The rule is applied simultaneously in all the cells, and the process is iterated for
t time steps.
In the most frequently studied version of this problem, N =
149 and the neighborhood is 7 (the central cell is represented by “u”; the
r = 3 cells to the left are represented by “c”, “b”, and “a”; the
r = 3 cells to the right are represented by “1”, “2”, and “3”).
Figure 4.14 shows a CA with N = 11 in which the updated state for the cellular automaton “u” is shown.
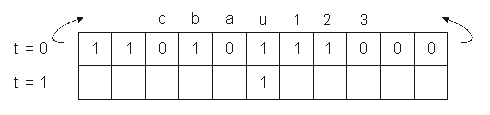
Figure 4.14. A one-dimensional, binary-state, r = 3 cellular automaton with
N = 11. The arrows represent the periodic boundary conditions. The updated state is shown only for the central cell. The symbols used to represent the neighborhood are also shown.
The task of density-classification consists of correctly determining whether ICs contain a majority of 1’s or a majority of 0’s, by making the system converge, respectively, to an all 1’s state (black or “on” cells in a space-time diagram), or to a state of all 0’s (white or “off” cells). As the density of an IC is a function of
N arguments, the actions of local cells with limited information and communication must be coordinated with one another in order to classify correctly the ICs. Indeed, to find, by hand, in a search space of
2128 transition states, rules that perform well, is an almost impossible task and, therefore, several algorithms were used to evolve better than human-written rules
(Das et al. 1994; Juillé and Pollack
1998; Koza et al. 1999; Ferreira
2001). The best rules with performances of 86.0% (Coevolution2) and 85.1%
(Coevolution1) were discovered using a coevolutionary approach between ICs and rules evolved by a GA (Juillé and Pollack
1998). The rules evolved by GEP are better than all the human-written rules and better than the GP rule or the rules evolved by the GA
(Mitchell et al. 1993 and Mitchell et al.
1994), and were discovered using computational resources that are more than 60,000 times smaller than those used by GP.
|
