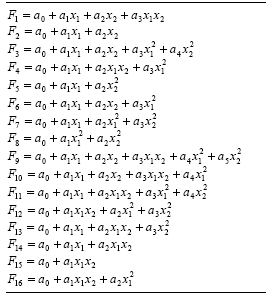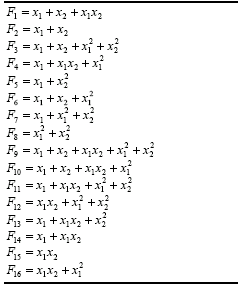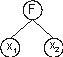
corresponds to:

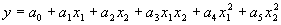
(4.22)

for the second-order bivariate basis polynomial function. The coefficients a₀ - a₅ can be easily evolved using a special domain Dc containing random constants. As before, the Dc comes after the tail but, in this case, has a length equal to 6h. Consider, for instance, the chromosome below with h = 2 (the Dc is shown in blue):

01234567890123456
FFabc252175089728	(4.23)

For the set of numerical constants:

A = {-0.606, -0.398, -0.653, -0.818, -0.047, 0.036, 0.889, 0.148, -0.377, -0.841}

its expression gives:

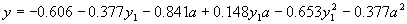
(4.24)

where .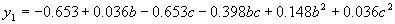

The two-parameter function “F” described here is the one used in STROGANOFF (Ivakhnenko 1971) which composes complete bivariate basis polynomial functions. In Table 4.15, this function is represented by F₉. The implementation of minor variants such as the incomplete bivariate basis polynomial functions used in the enhanced STROGANOFF (Nikolaev and Iba 2001) is also very simple. All these functions are shown in Table 4.15.

Table 4.15
Bivariate basis polynomials.

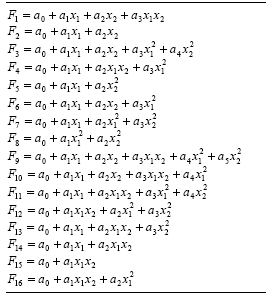
Another function easily implemented is the following:

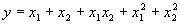
(4.25)

which, except for the coefficients, is identical to the function (4.22) or function F₉ in Table 4.15. This and similar functions based on the 16 bivariate functions of Table 4.15 are going to be included in the function kit of GEP in order to analyze the importance of numerical constants in the evolution of polynomials. Their description is given in Table 4.16.

Table 4.16
Bivariate basis polynomials with unit coefficients.

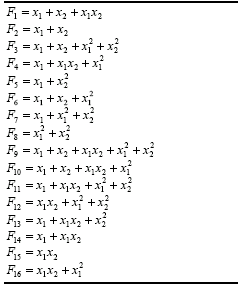
So, by choosing a function set consisting exclusively of function F₉ of Table 4.15, we are exactly simulating a STROGANOFF system in GEP. And by choosing a function set containing functions F₁ - F₁₆ of Table 4.15 we are exactly simulating an enhanced STROGANOFF system. The performance of these systems is analyzed in the next section.

As stated previously, the implementation of both STROGANOFF systems (the original and the enhanced) in gene expression programming requires a Dc length six times the head length due to the number of coefficients needed for the polynomials. Thus, it is convenient to use a slightly different notation to represent the random constants corresponding to each coefficient. For instance, for the gene below with an h = 4:

012345678
NOeEgbcaj	(4.26)

a Dc with length 24 is already necessary. If we choose a set of random numerical constants with 20 members and represent them by R = {r₀, ..., r₁₉}, the following structure will be a valid Dc domain for chromosome (4.26) above:

r19r12r15r9r2r19r13r6r5r19r12r7r17r10r7r15r7r18r9r11r15r16r1r17

As before, the values of all the random constants are kept in an array and are retrieved as needed.

Due to the huge dimensions of the random constants domains, it is important to be able to control the degree of genetic variation in them. Consequently, special mutation operators were implemented that allow the autonomous control of the mutation rate both on the head/tail domain and on the Dc domain. The other operators remain unchanged and work exactly as described in section 4.2.