The chromosomes we studied so far, the most common in GEP, are ideal for solving a wide range of problems. We may think of them as the core of GEP. However, there are other kinds of chromosomes with different structural and functional organizations,
especially designed to solve different classes of problems. In this section I present the structure of some of these chromosomes in order to show how GEP chromosomes can be easily modified to evolve solutions to very different types of problems.
Thus, the simplest chromosome will code for a single gene, composed of only one terminal, for instance:
Indeed, this kind of gene is obtained when h = 0 and n = 0. The length of the tail can be easily evaluated by equation
(2.4), giving t = 1 and, therefore,
g = 1. Although of little use in unigenic chromosomes, these simple genes or even ORFs composed of only one element are important when integrated in a more complex chromosome.
In fact, one-element ETs can be found not only as the expression of one-element genes but also as the expression of bigger genes with head lengths greater than 0. For instance, in the following three-genic chromosome, gene 2 codes for a one-element ORF (the tails are shown in
blue):
| 012345678901201234567890120123456789012 |
|
|
Q+aaa/babbabaa+*b+-bababbb-***aabaaaaba |
(2.11) |
The three sub-ETs encoded in this chromosome are shown in Figure
2.3.
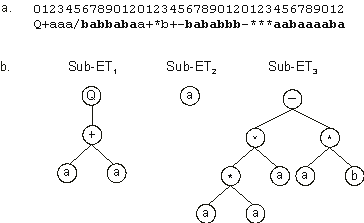
Figure 2.3. A three-genic chromosome encoding a one-element sub-ET
(sub-ET2). a) The three-genic chromosome with the tails shown in bold.
b) The sub-ETs codified by each gene.
Notwithstanding, in multigenic systems, one-element genes are extremely useful as they can be organized in multigene families (MGFs). These multigene families consist of clusters of related genes encoding, for instance, a particular class of variables. Thus, in MGFs, each gene codes for a particular terminal or task. We will see that such chromosomes composed of MGFs are very useful for evolving solutions to scheduling problems
(chapter 6). For instance, the different cities in the traveling salesperson problem can be encoded in a multigene family, where each gene codes for a city. Consider the simple chromosome below, composed of one MGF with nine members:
| 012345678 |
|
|
GCDAHEIFB |
(2.12) |
where each element represents one city. In this case, the expression consists of the spatial organization of the sub-ETs, i.e., the orderly way in which they interact with one another
(Figure 2.4). We will see in chapter
6 that the expression of this kind of chromosome can be used to encode a tour for the traveling salesperson problem.
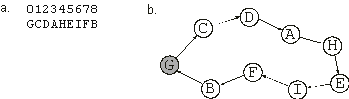
Figure 2.4. Expression of one-element genes as a spatial organization of sub-ETs. If each symbol represented a city visited by a salesperson, the complete expression of the chromosome in
(a) would correspond to the nine-city tour shown in (b). The starting and finishing city is shown in gray.
However, for more complicated scheduling problems, more than one MGF can be used and, for those problems, the chromosomes may contain two or more MGFs. For instance, the chromosome below was designed to evolve solutions to a simple assignment task (multigene families have different
colors):
| 012345012345 |
|
|
453621DABFEC |
(2.13) |
In chapter 6 we will see how these chromosomes are expressed and the kind of interactions they can encode. Although the examples presented in this book involving multigene families are very simple, they show that MGFs could be very useful in solving a wide range of scheduling problems.
One-element genes are also important to solve other kinds of problems, where the products of these simple genes are linked posttranslationally by a chosen function. For instance, complex Boolean functions can be modeled using this kind of chromosomal organization. The example below is a chromosome of nine one-element genes, where the sub-ETs are linked three by three with the Boolean function IF
(x, y, z) (if x = 1, then return y; else return
z):
| 012345678 |
|
|
bbcaedcff |
(2.14) |
The symbols {a, b, c, d, e, f} represent the six arguments of a Boolean function. Its expression is shown in
Figure 2.5.
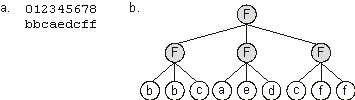
Figure 2.5. Expression of clusters of one-element genes as Boolean functions.
a) A chromosome composed of nine one-element genes. b) The one-element sub-ETs posttranslationally linked by a three-argument function “F”.
The examples above are examples of chromosomes that are simpler than the basic GEP chromosome described in
section 2.1.3. However, in GEP, there are other chromosomal organizations which are still more complex than the basic multigenic chromosome. These complex chromosomes consist of clusters of functional units composed of conventional head/tail domains plus one or more extra domains. The extra domains usually code for several one-element sub-ETs. All the sub-ETs encoded in the different domains interact with one another, forming a more intricate entity. These chromosomes were designed to solve symbolic regression problems using numerical constants (see
chapter 4, section
4.2) and to evolve complex neural networks, where the extra domains code for the weights and thresholds of a neural network (see
chapter 5). For example, the chromosome below of length 34 is composed of two genes, each with a head of length 2, a tail of length 7, and an extra domain of length 8 encoding the weights of a neural network (the genes are shown in different
colors):
| 0123456789012345601234567890123456 |
|
|
Tbababaab29418263DQbabaaba55157646 |
(2.15) |
The symbols “D”, “T”, and “Q” represent, respectively, a function of two arguments, a function of three arguments, and a function of four arguments. In each gene, the domain encoding the weights goes from position 9 through 16, and the numerals are symbols representing the weights for the neural net encoded in the respective head/tail domain. The complex pattern of expression of such chromosomes is explained in
chapter 5.
Depending on the problem at hand, other chromosomes may be designed in order to encode more domains. For example, if we wanted to evolve the thresholds of a neural network as well, a second domain could be created (the domains have different
colors):
| 0123456789012345678 |
|
|
QDabaabbb0810088324 |
(2.16) |
In this single-gene chromosome, the first extra domain goes from position 9 through 16 and encodes the weights, whereas the second goes from position 17 through 18 and encodes the thresholds for the neural net encoded in the head/tail domain.
In summary, the gallery of chromosomes presented in this section is an illustration of the plasticity of the genotype/phenotype representation of GEP and may serve as an inspiration in designing different chromosomal architectures to evolve solutions to very different problems.
|


