Genetic Programming, invented by Cramer in 1985 (Cramer
1985) and further developed by
Koza (1992), finds an alternative to fixed length solutions
through the introduction of nonlinear structures (parse trees) with
different sizes and shapes. The alphabet used to create these
structures is also more varied than the 0ís and 1ís of GAsí
individuals, creating a richer, more versatile system of
representation. Notwithstanding, GP individuals also lack a simple,
autonomous genome: like the linear chromosomes of GAs, the nonlinear
structures of GP are also naked replicators cursed with the dual
role of genotype/phenotype.
It is worth noticing that the parse trees of GP resemble protein
molecules in their use of a richer alphabet and in their complex and
unique hierarchical representation. Indeed, parse trees are capable
of exhibiting a great variety of functionalities. The problem with
these complex replicators is that their reproduction with
modification is highly constrained in evolutionary terms, simply
because the modifications must take place on the parse tree itself
and, consequently, only a limited range of modification is possible.
Indeed, the genetic operators of GP operate at the tree level,
modifying or exchanging particular branches between trees.
Although at first sight this might appear advantageous, it greatly
limits the GP technique (we all know the limits of grafting and
pruning in nature). Consider, for instance, crossover, the most used
and often the only search operator used in GP (Figure 1).
In this case, selected branches are exchanged between two parent
trees to create offspring. The idea behind its implementation was to
exchange smaller, mathematically concise blocks in order to evolve
more complex, hierarchical solutions composed of simpler building
blocks, guaranteeing, at the same time, the creation of
syntactically correct structures.
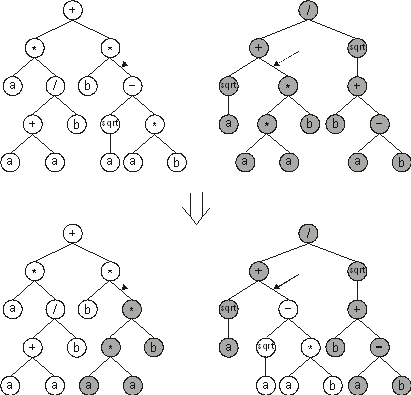
Figure 1. Tree crossover in Genetic Programming. The
arrows indicate the crossover points.
The mutation operator in GP is also very different from natural
point mutation. This operator selects a node in the parse tree and
replaces the branch underneath by a new randomly generated branch (Figure 2).
Notice that the overall shape of the tree is not greatly changed by
this kind of mutation, especially if lower nodes are preferentially
chosen as mutation targets.
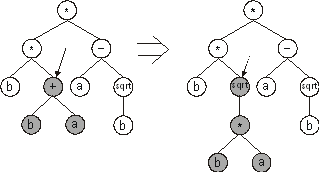
Figure 2. Tree mutation in Genetic Programming. The arrow indicates the mutation point. The new branch randomly generated by the mutation operator in the daughter tree is shown in gray.
Permutation is the third operator used in Genetic Programming and
the most conservative of the three. During permutation, the
arguments of a randomly chosen function are randomly permuted (Figure 3).
In this case the overall shape of the tree remains unchanged.

Figure 3. Permutation in Genetic Programming. The arrow indicates the permutation point. Note that the arguments of the permuted function traded places in the daughter tree.
In summary, in Genetic Programming the operators resemble more of
a conscious mathematician than the blind way of nature. But in
adaptive systems the blind way of nature is much more efficient and
systems such as GP are highly limited in evolutionary terms. For
instance, the implementation of other operators in GP, such as the
simple yet high-performing point mutation (Ferreira 2002c),
is unproductive as most mutations would have resulted in
syntactically incorrect structures (Figure 4).
Obviously, the implementation of other operators such as
transposition or inversion raises similar difficulties and the
search space in GP remains vastly unexplored.
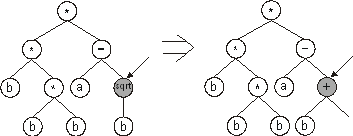
Figure 4. Illustration of a hypothetical event of point mutation in
Genetic Programming. The arrow indicates the mutation point. Note that the daughter tree is an invalid structure.
Although Koza described these three operators as the basic GP
operators, crossover is practically the only genetic operator used
in most GP applications (Koza 1992,
1994;
Koza et al. 1999). Consequently,
no new genetic material is introduced in the genetic pool of GP
populations. Not surprisingly, huge populations of parse trees must
be used in order to prime the initial population with all the
necessary building blocks so that good solutions could be discovered
by just moving these initial building blocks around.
Finally, due to the dual role of the parse trees (genotype and
phenotype), Genetic Programming is also incapable of a simple,
rudimentary expression; in all cases, the entire parse tree is the
solution: nothing more, nothing less.
|



