To solve the sequence induction problem without the facility to manipulate numerical constants, the function set was exactly the same as in the experiment with random constants. The terminal set consisted obviously of the independent variable alone.
As shown in the second column of Table 2, the probability of success using this approach is 81%, considerably higher than the 16% obtained using the facility to manipulate random constants. In this experiment, the first perfect solution was found in generation 44 of run 0 (the contribution of each sub-ET is indicated in square brackets):
|
y = [2a] + [a3 + a] +
[a4 + 3a3 + 2a2]
+ [4a4] + [1] + [a2 - a] + [0] |
(3.6) |
which is equivalent to the target sequence (3.1). In this case the algorithm created all the necessary constants from scratch by performing simple mathematical operations.
To find the “V” shaped function without using random constants, the function set is exactly the same as in the first approach. With this collection of functions, most of which extraneous, the algorithm is equipped with different tools for evolving highly accurate models without using numerical constants. The parameters used per run are shown in the fourth column of
Table 2. In this experiment of 100 identical runs, the best solution was found in generation 4679 of run 10 (the contribution of each sub-ET is indicated in square brackets):
|
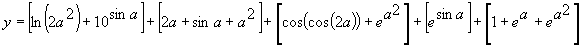
|
(3.7) |
It has a fitness of 1990.023 and an R-square of 0.9999313 evaluated over the set of 20 fitness cases and an R-square of 0.9998606 evaluated against the same testing set used in the first approach, and thus is better than the model
(3.4) evolved with the facility for the manipulation of random constants.
To predict sunspots without using random numerical constants, the function set is exactly the same as in the first approach. The parameters used per run are shown in the sixth column of
Table 2. In this experiment of 100 identical runs, the best solution was found in generation 2273 of run 57:
|
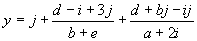
|
(3.8) |
It has a fitness of 89176.61 and an R-square of 0.882831 evaluated over the set of 90 fitness cases, and thus is better than the model
(3.5) evolved with the facility for the manipulation of random constants.
It is instructive to compare the results obtained in both approaches. In all the experiments the explicit use of random constants resulted in a worse performance. In the sequence induction problem, success rates of 81% against 16% were obtained; in the “V” function problem average best-of-run fitnesses of 1931.84 versus 1914.80 and average best-of-run R-squares of 0.995340 versus 0.957255 were obtained; and in the sunspots prediction problem average best-of-run fitnesses of 89033.29 versus 86215.27 and average best-of-run R-squares of 0.811863 versus 0.713365 were obtained (see
Table 2). Thus, in real-world applications where complex realities are modeled, of which nothing is known concerning neither the type nor the range of the numerical constants, and where most of the times it is impossible to guess the exact function set, it is more appropriate to let the system model the reality on its own without explicitly using random constants. Not only the results will be better but also the complexity of the system will be much smaller.
|