A neural network with all its elements is a rather complex structure, not easily constructed and/or trained to perform a certain task. Consequently, several researchers used sophisticated algorithms in which a GA was used to evolve partial aspects of neural networks, such as the weights, the network architecture, and the learning algorithm (see
Whitley and Schaffer 1992 for a collection of articles on neural networks and
GAs).
Due to the simplicity and plasticity of gene expression programming, it is possible to fully encode complex neural networks of different sizes and shapes in linear chromosomes of fixed length. Furthermore, these complex structures are fully functional, that is, they can adapt in a particular environment and, thus, can be selected according to fitness. And this means that populations of these entities can be used to explore a search space and, therefore, evolve solutions to very different problems.
In GEP nets, the network architecture is encoded in the familiar structure of a head/tail domain. The head contains special functions that activate the hidden and output units (in the GEP context, more appropriately called functional units) and terminals that represent the input units. The tail contains obviously only terminals. Besides the head and the tail, these genes (neural net genes or NN-genes) contain two additional domains, Dw and Dt, encoding, respectively, the weights and the thresholds. Structurally, the Dw comes after the tail and has a length
dw equal to hn, whereas the Dt has a length
dt equal to h. Both domains are composed of symbols representing the weights and thresholds of the neural net.
For each NN-gene, the weights and thresholds are created at the beginning of each run, but their circulation is guaranteed by the genetic operators. Furthermore, special mutation operators were created that allow the permanent introduction of variation in the set of weights and thresholds.
It is worth emphasizing that the basic genetic operators such as mutation, IS and RIS transposition, are not affected by Dw or Dt as long as the boundaries of each region are maintained and the alphabets of each domain are used correctly within the confines of the respective domains.
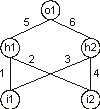
Consider the conventionally represented neural network with two input units
(i1 and i2), two hidden units (h1 and
h2), and one output unit (o1) (for simplicity, the thresholds are all equal to one and are omitted):
It can also be represented by a conventional tree:
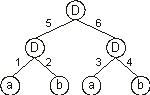
where a and b represent, respectively, the two inputs
i1 and i2 and “D” represents a function with connectivity two. This function multiplies the values of the arguments by the respective weights and adds all the incoming activation in order to determine the forwarded output. This output (zero or one) depends on the threshold, that is, if the total incoming activation is equal to or greater than the threshold, then the output is one, zero otherwise.
We could linearize the above NN-tree as follows:
|
0123456789012
DDDabab654321 |
where the structure in blue encodes the weights. The values of each weight are kept in an array and are retrieved as necessary. For simplicity, the number represented by the numeral in Dw indicates the order in the array.
Let us now analyze a simple neural network encoding a well-known function, the exclusive-or. Consider, for instance, the chromosome below with
h = 3 and a domain encoding the weights with dw = 6 (the Dw is shown in
blue):
|
0123456789012
DDDabab393257 |
Its translation gives:
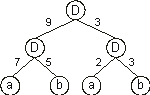
And for the set of weights:
|
W = {-1.978, 0.514, -0.465, 1.22, -1.686, -1.797, 0.197, 1.606, 0,
1.753} |
the neural network above gives:
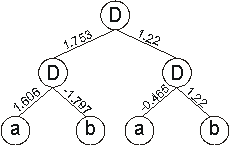
which is a perfect solution to the exclusive-or function.
|



